
Q-Learning의 Q는 무슨 의미?
이 질문에 답하려면 먼저 통계의 P 값 (P -Value)에 대해 알아야 합니다. 우선 P 값의 설명부터 시작합니다. P 값 (P -Value )는
P 값 (P -Value) 이란?
세상에는 "증명하고 싶은 가설"이 많이 있습니다. '세차를 하면 비가 온다'는 등의 가설은 아마 기분 탓일 겁니다. 하지만 "IT 업계에는 B형이 많다"라는 가설은 내심 그런 것 같기도 하고 알아보고 싶은 생각이 듭니다(사실 저도 B형). 통계를 통해서 이러한 가설들을 입증하는 방법이 가설 검정입니다.
한국인의 B형의 비율은 21.9%입니다. 만약 IT기업의 건강 조합에서 B형인 사람들의 통계를 살펴본다면, "IT업계에 B형이 많다"라는 가설이 맞는지 알 수 있을 것 같네요. 이와 같이 증명하고 싶은 가설을 대립 가설(Alternative hypothesis)이라고 하고 대립 가설을 부정하는 쪽을 귀무가설(Null hypothesis)이라고 합니다. 이 경우는 "IT업계도 B형의 비율은 그렇게 다르지 않다"라는 것이 귀무가설이 되겠군요. 그리고 대립 가설을 증명하기 위해 귀무가설이 틀렸다는 것을 증명하는 귀류법이 통계에서는 자주 사용됩니다.
귀무가설인 '그렇게 다르지 않다'를 측정하는 척도가 P입니다. P는 Probability의 P, 즉 "확률"을 나타내는 수치입니다. 그리고 이 '그렇게'를 구체적으로 확인하기 위해 P값의 임계값이 설정됩니다. 예를 들어 임계값이 0.05인 경우 '그렇게'는 5%입니다.
구체적인 예로 설명하겠습니다.
건강 조합의 사람이 100,000 명 있다고 합시다. B형의 비율이 21.9%라는 것은 21,900명 정도가 B형이라면 귀무가설이 옳다고 증명됩니다. 딱 맞게 21,900명은 아닙니다. 예를 들어 오차 5% 이내라면 21,900명 내외로 간주합니다. 여기서 말하는 5%의 오차는 21,900 × 0.05 = 1,095명처럼 간단한 계산이 아닙니다. 어디까지나 통계이므로 그림 2와 같이 정규 분포에서 양쪽 2.5%씩의 범위에 포함되는지 여부로 판정합니다.
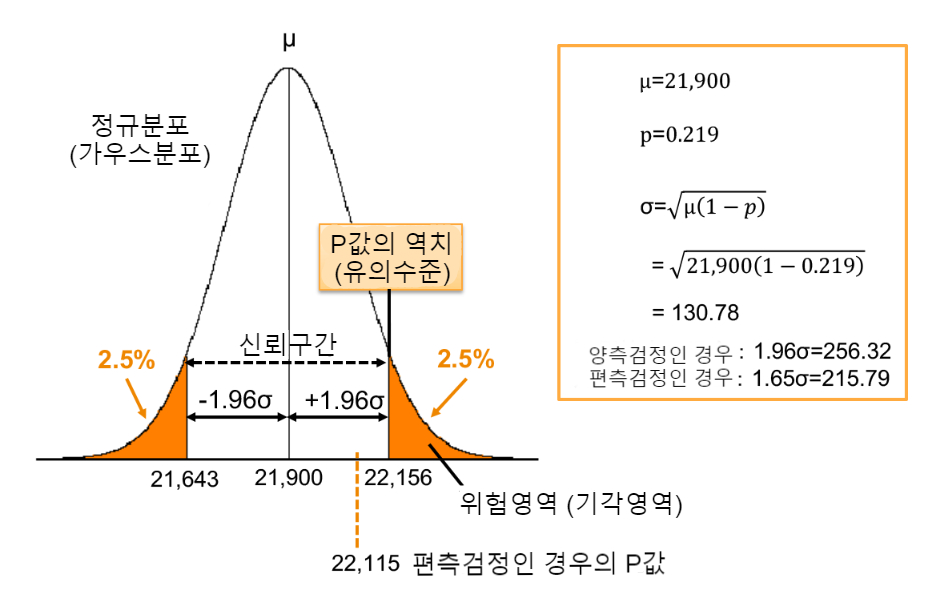
정규 분포(가우스 분포라고도 함)는 확률 분포입니다. 즉, 그림 1에서 양쪽 2.5%보다 안쪽(신뢰 구간)이라면, "글쎄, 확률적으로 우연히 있을 수 있는 일"이라 판단하고, 그 바깥은 "역시, 우연이라 하기엔 억지가 있다"라는 것입니다. 이 판단의 역치(임계값)를 결정하는 값이 P 값이며, 예로 P 값이 0.03이라면 양쪽은 1.5%가 됩니다.
P 값은 이 바깥쪽이라면 이제 더 이상 우연이라 할 수 없고, 뭔가 의미가 있다는 의미이므로 유의 수준이라고도 합니다. 그리고 그 바깥쪽은 귀무가설이 옳음에도 불구하고 5%의 확률로 잘못된 대립 가설을 채택해 버리는 영역이므로 위험 지역이라고 합니다(최근에는 귀무가설을 기각하는 영역이므로 기각역이라고도 합니다). 한편, 안쪽의 범위는 신뢰 구간이라고 합니다.
잘못된 판정을 할 가능성은 두 가지가 있습니다.
하나는 "사실 그다지 다르지 않지만, IT업계에는 B형이 많다고 판단"하는 Fales Positive(FP)
다른 하나는 "사실 IT업계에는 B형이 많지만, B형의 비율은 그다지 다르지 않다고 판단"하는 Fales Negative (FN) (그림 2).
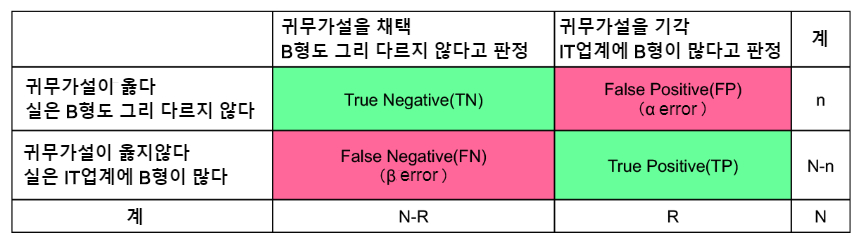
FWER = FP/(TN+FP)... 확률
'실은 귀무가설이 옳지만 기각되어 버리는 데이터의 경우'
(실은 B형도 그리 다르지 않은데, IT업계에 B형이 많다고 판정해 버리는 데이터의 경우)
FDR = FP/(TP+FP)... 기대치
'기각된 귀무가설이 실은 옳은 데이터인 경우'
(IT업계에 B형이 많다고 판정한 속에, 실은 B형도 그리 다르지 않다는 데이터도 포함되어 있는 경우)
IT기업의 건강 조합에서 조사한 결과, B형인 사람이 22,166명이었다고 합시다. 그림 2와 대조하면 이 값은 유의 수준보다 10명이 많으므로 귀무가설이 틀린 것이 되어버리고, 대립 가설(IT업계에는 B형이 많다)이 잘못되었다고 판단하지 못합니다.
만약 B형이 22,150명이었다면 어떨까요. 이번에는 유의 수준을 초과하지 않으므로 귀무가설이 옳고 대립 가설은 잘못된 것으로 판정됩니다.
유의 수준을 초과하지 않은 경우, 대립 가설은 부정당합니다. 한편, 우위 수준을 초과하는 경우는 대립 가설을 옳다고 판정하는 것이 아니라, "부정할 수 없다"는 관공서 같은 답변입니다. 하지만 유의 수준을 초과하지 않은 경우에도, 사실은 IT업계에 B형이 많은데도 B형의 비율은 그렇게 다르지 않다고 판정해 버리는 Fales Negative(FN)가 생길 가능성이 있습니다.
또한 임계치 판정은 양측 검정과 단측 검정이 있습니다. 만약 반드시 값이 크다는 것이 자명한 경우에 P 값을 0.05로 한 경우, 큰 쪽에만 5%가 위험영역이 됩니다. 만약 동일하게 0.05로 단측을 하면 P 값의 한계는 22,115명이 되므로 22,150명이 위험 영역에 들어가게 되는 것입니다.
| 값과 유의 수준 P 값과 유의 수준의 관계가 오해받기 쉽기 때문에 설명을 보충합니다. P 값은 특정 값이 정규 분포(확률 분포)의 어딘가에 해당하는지 나타내는 확률입니다. 예를 들어, 22,166명의 P 값은 0.4이므로, 나머지 2%의 확률 영역에 있다는 것을 나타내고 있습니다. 한편, 유의 수준은 "임계치로서의 P 값"입니다. 무엇이 혼란스러운가 하면, 일반적으로 이 임계치를 단순히 P 값으로 읽고, 'P 값 = 유의 수준'이라 쓰기 때문에 'P 값 = 역치'라고 착각하기 쉽습니다. 엄밀하게 말하면, P 값의 임계치 = 유의 수준입니다. 이 점을 이해한 후 생략되어 있는 역치라는 문자를 보충해서 판별하십시오. |
다중 검정과 FWER
이제 가설 검정에 있어서의 P에 대해 알았으니 Q로 넘어가고 싶지만, 그전에 다중 검정과 FWER를 설명해야 합니다. 단지 Q를 설명할 뿐인데 이번에는 서론이 깁니다.
IT기업의 건강 조합은 여럿 있으므로 4개의 조합에서 각각 100,000명의 혈액형을 조사했습니다. 그 결과, 4개의 건강 조합 중 하나만 '유의'인 경우, "IT업계에 B형이 많은 것은 부정할 수 없다"라고 해도 좋은 것일까요?
샘플(건강 조합)이 4개인 경우, 어느 하나가 '유의'가 될 확률은 다음의 계산에서 18.5%입니다. 하나의 조합만으로 측정하는 경우 유의가 될 확률(p = 0.05)에 비해 발생 확률은 3.7배에 달합니다. 따라서, 4개 중 하나의 조합이 '유의'였다고 해도, 그것을 가지고 "IT업계에는 B형이 많은 것을 부인할 수 없다"라고 하기에는 어려울 것입니다. 하지만 조합의 하나는 '유의'이기 때문에 "IT 업계에서도 B형의 비율은 그렇게 다르지 않다'는 귀무가설도 입증되었다 말하기는 어려운 것입니다.
1- (1-p) ^ 4 = 1- (1-0.05) ^ 4 = 0.185
이처럼 여러 샘플에서 '유의'가 되는지 여부를 확인하는 것이 다중 검정입니다. 그리고 다수의 검정 중 어느 하나가 '유의'가 될 확률을 FWER(familywise error rate)라고 합니다. 다중 검정에 있어서는, 하나의 검정으로 '유의'가 되는 P 값이 아니라, FWER을 컨트롤해야 하는(예 FWER 18.5 → 5%)라는 개념이 사용되고 있습니다.
FDR
FWER는 그림 2의 FP / (TN + FP)를 작게 하려는 접근입니다. 사실은 귀무가설이 올바른 경우 귀무가설을 기각해 버리는 비율, 즉 "사실은 B형도 그렇게 다르지 않지만, IT업계는 B형이 많다고 판단해 버리는 비율"을 다중 검정을 통해 컨트롤하기 위한 지표입니다.
일련(family)의 검정에서 1개도 '유의'가 되지 않을 확률(FWER)을 줄이려면, 다중성이 늘어날수록 각 검정의 유의 수준 P를 줄여야 합니다. 그리고 유의 수준 P를 엄격하게 하면 이번에는 FN(β 오류) '사실은 IT 업계에 B형이 많지만, B형도 그렇게 다르지 않다고 판정해 버리는 오류'가 발생하기 쉬워집니다.
이 문제를 해결하기 위해 다중성에 따라서 어느 정도는 틀려도 좋다는 발상에서 등장한 것이 FDR(false discovery rate)입니다.
FDR는 FP / (TP + FP)의 비율을 구하는 방법으로 FP(α 오류)를 어느 정도 허용합니다. 귀무가설이 기각된 가운데, 사실은 귀무가설이 올바른 비율, 즉 "IT업계에 B형이 많다고 판단한 가운데, 실은 B형도 그렇게 다르지 않다는 데이터도 포함되어 있는 비율"을 컨트롤하는 지표입니다.
우리는 신이 아니기 때문에 어떤 데이터가 TN, FP, FN, TP인지 잘 모릅니다. 그래서 FDR는 기대치로 구합니다. P(Provability) 값이 확률인데 반해, FDR는 기대치인 것입니다. 유의 수준 P와의 관계로 말하자면, FWER을 작게 하기 위해서는 P를 작게 할 필요가 있으며, P를 크게 하면 FWER은 커집니다. 한편 FDR 쪽은 P를 크게 하면 FDR은 커지고, P를 작게 하면 FDR은 작아집니다.
FDR을 제어하는 방법에는 여러 가지가 있지만, 가장 유명한 BH(Benjamini-Hochberg)법을 알아봅시다.
Benjamini-Hochberg(BH 법)
BH 법은 FDR을 제어하는 방법의 하나입니다. BH법 중에서도 몇몇 보정 방식이 있는데, 표준적인 계산 방법을 4가지의 건강 조합의 예를 통해 설명합니다.
① N개의 귀무가설(4가지 건강 조합) 각각의 B형인 비율 P 값을 계산한다.
건강 조합 1은 22,166명 이므로 P 값은 0.04. 다른 건강 조합의 P값은 표 1과 같다고 합시다.
| 샘플 | P 값 |
| 건강 조합 1 | 0.04 |
| 건강 조합 2 | 0.16 |
| 건강 조합 3 | 0.08 |
| 건강 조합 4 | 0.01 |
표 1 : 4 개의 건강 조합에서 B형인 사람의 수 P 값을 계산
② P 값의 오름차순으로 정렬 순서를 i라고 합니다. (i = 1 ~ 4)
아래쪽 표 2와 같이 건강 조합 4, 1, 3, 2의 순서입니다.
③ FDR의 임계치를 결정합니다.
여기서는 0.05로 하고 있습니다. 5%이기 때문에 귀무가설이 100개 기각된 경우, 그 안에 진짜 귀무가설이 5개 들어있는 것을 허용하는 것이 됩니다.
④ 각 샘플의 p 값을 q 값으로 변환합니다. (N은 샘플의 수 = 4)
qi = pi × N / i
이 q가 FDR의 기대치입니다. p 값을 오름차순으로 정렬했을 때 q 값이 어떤 값이 될지를 그림 3과 같은 관계식으로 구하고 있습니다.
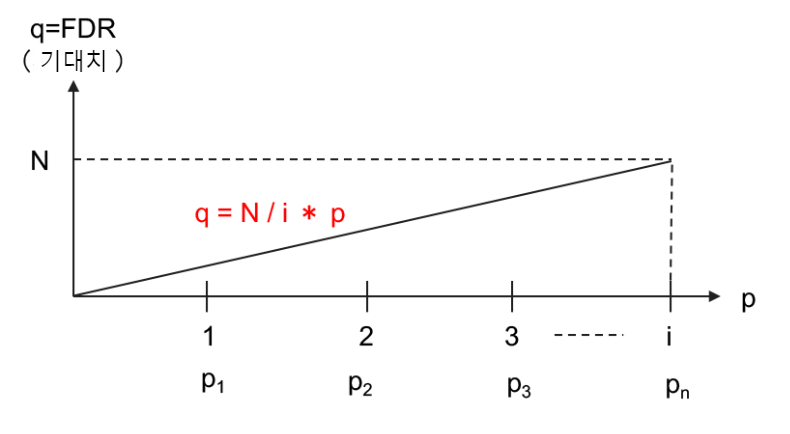
⑤ qi와 qi +1을 비교하여 qi > qi + 1 이면 qi = qi + 1 합니다.
⑥ qi와 임계치를 비교하여 기각 판정
qi <= 임계치라면 유의, 그렇지 않으면 기각합니다.
| 샘플 | pi | i | qi = pi x N/i | FDR의 역치 | qi 비교 역치 | 판정 |
| 건강조합4 | 0.01 | 1 | 0.01 x 4/1=0.04 | 0.05 | 0.04 <= 0.05 | 유의 |
| 건강조합1 | 0.04 | 2 | 0.04 x 4/2=0.1 | 0.05 | 0.1 > 0.05 | 기각 |
| 건강조합3 | 0.08 | 3 | 0.08 x 4/3=0.11 | 0.05 | 0.11 > 0.05 | 기각 |
| 건강조합2 | 0.16 | 4 | 0.16 x 4/4=0.16 | 0.05 | 0.16 > 0.05 | 기각 |
표 2 : P 값의 오름차순으로 정렬하여 기각 판정
이번 4개의 건강 조합의 데이터를 BH 법으로 계산한 결과, 표 2와 같이 4개의 귀무가설 중 하나는 '유의'가 되었습니다. 즉, FDR의 임계치가 0.05인 경우 위의 검정 결과는 "IT업계에서도 B형의 비율은 그렇게 다르지 않다"라고 말할 수 없는 것입니다. 또한, 표 2의 각 pi의 값을 P 값 0.05에서 각각 비교하면 건강 조합 4와 건강 조합 1이 '유의'가 되어, FDR과 다른 '유의'한 수가 됩니다.
FDR은 Family의 수(N개)가 많고, 귀무가설이 기각되는 수(R)가 많은 집합에 비해서 유용한 모델입니다. 예를 들어 10만 유전자에 약을 투여하여 영향이 있는 유전자를 선택하는 실험을 했다고 합시다. 10%에 변화가 생겼다면 1만 귀무가설이 기각된 것입니다. Q임계값이 5%라는 것은 이 1만 중에서 500 유전자 정도는 FP(α 오류)가 포함될 가능성이 있는 것입니다.
Q 값 (Q-Value) 란
오래 기다리셨습니다. 그림 4와 같은 흐름으로 이제야 간신히 Q 값을 설명할 수 있습니다. Q 값은 "검정 결과가 유의하다고 판단되는 최소의 FDR 임계치"입니다. 표 2는 임계치가 0.05로 유의이었지만, 임계치를 0.03로 낮춘 경우 어떤 qi도 기각됩니다. 이 경우 최대한 크게 되는 임계치는 0.04이므로 Q = 0.04가 되는 것입니다.

확률에서 요구되는 P 값의 임계치(유의 수준)가 P 값인데 반해, 기대치로서 요구되는 FDR의 임계치가 Q 값입니다. 그리고 P 는 Probability(확률)의 P 인데, Q 값은 "같은 임계치지만 P 와는 다른 임계치 이므로 Q 라고 해두자"라는 것입니다(이는 저의 견해로 Quality의 Q라는 설도 있습니다).
'AI · 인공지능 > 알기쉬운 AI' 카테고리의 다른 글
| [알기쉬운 AI - 27] 클러스터링 (Clustering) (0) | 2020.05.07 |
|---|---|
| [알기쉬운 AI - 26] 분류 (Classification) (0) | 2020.04.26 |
| [알기쉬운 AI - 25] 회귀 (Regression) (0) | 2020.04.25 |
| [알기쉬운 AI - 24] Q 학습 (Q-Learning) (0) | 2020.04.04 |
| [알기쉬운 AI - 22] 강화학습과 도적 알고리즘 (0) | 2020.03.18 |
| [알기쉬운 AI - 21] 과학습을 막는 방법 (0) | 2020.03.14 |
| [알기쉬운 AI - 20] 비정상적인 과학습 (0) | 2020.02.10 |
| [알기쉬운 AI - 19] 머신 러닝의 학습 데이터 (0) | 2020.02.08 |



