지난번에는 "Q-Learning의 Q는 무엇의 약자인가요?"라는 질문에 대하여, "검정 결과가 유의하다고 판단되는 최소의 FDR(false discovery rate)의 수"임을 알 수 있었습니다. 이번에는 드디어 Q-Learning의 학습 방법에 대해 알아봅시다.
해전 게임
Q-Learning의 구조는 "해전 게임"과 비슷합니다. 이것은 2명이 하는 대전형 게임입니다. 종이에 그림 1(R)과 같이 그리고 상대방이 모르게 자신의 함대를 배치합니다(전함과 순양함과 잠수함 3척의 함대입니다).

상대가 선공이라고 합시다. 상대방이 "3의 C"라고 어뢰를 맞출 위치를 지정해서 공격해 왔을 경우, 거기에 내 함이 있었다면 "명중"이라고 밝히고 내 전함은 침몰합니다. 이번에는 명중이 아니라 S(잠수함)의 주변이므로, "파도 상승"이라고 힌트를 주면서 살짝 아까웠다는 사실을 상대방에게 알려줍니다.
다음은 이쪽의 공격입니다. "2의 D"를 공격해 보았는데 "파도 상승"이라는 응답이 있었으므로, 전략 보드(상대방 쪽) 2의 D에 '파도'라고 표시해 둡니다. 이제 상대의 군함이 주변에 있다는 것을 알 수 있습니다.
이런식으로 서로 공격하는 것입니다만, 반복적으로 공격하다 보면 전략 보드(Q)의 정보가 풍부해져 점차 상대방의 나머지 함들의 위치가 보이게 됩니다. 그리고 먼저 상대를 전멸시키면 승리하는 게임입니다. PC도 스마트폰도 없던 시대에 연필과 종이만 있으면 간단하게 할 수 있는 소년의 마음을 자극하는 놀이였습니다.
Q-Learning 이란?
그럼, 해전 게임을 이해한 시점에서 Q-Learning의 개념을 알아봅시다. Q-Learning을 이해하는 데 있어서 유명한 5개의 방 튜토리얼이 있는데요, 여기서는 그것을 오마주 하여 6개의 방으로 이루어진 "영희 구출 미션"을 통해 설명해 보겠습니다(그림 2).

그림에는 A에서 F까지 방이 있습니다. 에이전트는 A방에서 시작하여 F방에 감금되어 있는 영희를 구하러 갑니다. 방에서 방으로의 이동 관계를 나타내면 그림 3과 같이 됩니다. 이때, "영희를 만나는 경우"의 이동에 대해서는 보상값 100을 주고 그렇지 않으면 보상값을 0으로 합니다. 영희가 있는 F방에서 F방으로의 이동(즉, 스테이)도 가능하다고 합시다.
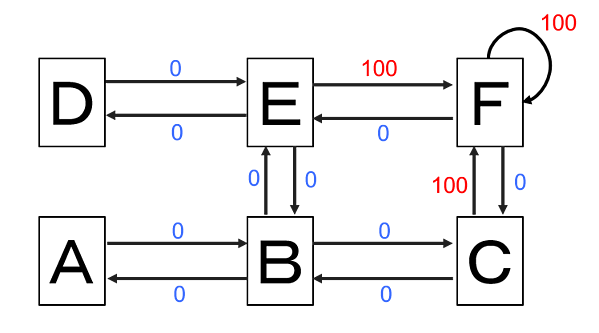
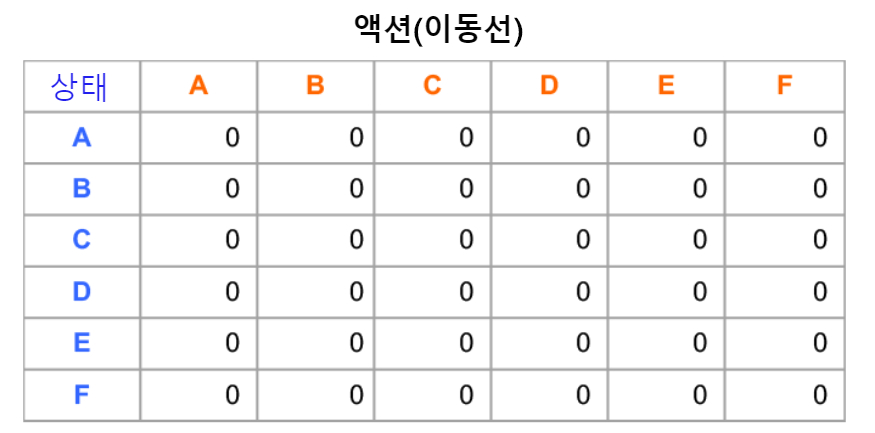
또한 이것을 행렬로 어레인지 한 것이 그림 4R입니다. 상태(지금 있는 방)와 액션(이동)을 매트릭스로 나타내서 어디서 어디로 이동하면 즉시 보상을 얻을 수 있는지 관계를 나타냈습니다.

Q-Learning에서는 훈련을 통해 '어디로 이동하면 골에 접근하는가'라는 정보를 기억해 갑니다. 보상은 F방에 도달하여 영희를 구출하는 것입니다. 따라서 상태를 나타내는 (R)표 외에 경험(탐색)하여 얻은 지식을 기록하는 전략 보드(Q보드)를 제공합니다. 초기 상태에서는 아직 아무것도 경험하지 않았기 때문에 Q보드는 그림 4Q처럼 모두 0입니다. 학습을 진행해 가면서 이 Q보드에 유용한 정보가 기록되어 가고, 그 결과로 Q보드를 보며 플레이 함으로써 효율적으로 최대의 보상을 얻을 수 있는 것입니다(해전 게임과 같네요).
Q보드에 정보를 기록하는 규칙
Q보드에 정보를 기록하는 기본 규칙은 아래와 같습니다.
① 초기 상태에서 Q보드는 모두 0으로 합니다.
② Q를 구하는 계산식을 설정합니다.
Q(상태, 액션) = R(상태, 액션) + γ × Max (Q (다음 상태, 모든 액션))
③ γ(감마) 매개변수와 보상을 결정합니다.
γ는 할인율이라고 하며 범위는 0 ~ 1입니다.
0에 가까울수록 즉각적인 보상을 중시하는 경향이 있습니다.
γ = 0.8
보상 = 100
④ 에피소드(학습)를 여러번 반복하여 에피소드 종료시마다 Q보드에 값을 기록합니다.
⑤ 1개의 에피소드는 무작위로 지정된 상태(방)에서 시작하며, 최대의 보상(F방)에 도착한 시점에서 종료합니다.
⑥ 1개의 에피소드는 다음과 같은 처리로 진행합니다.
1. 랜덤으로 6개의 방 중 어딘가를 탐색의 시작 위치로 합니다.
2. 현재 방에서 이동할 수 있는 액션 중에서 하나를 선택합니다.
3. Q값을 ③의 식으로 계산하여 Q보드를 업데이트합니다.
4. 이동의 도착지가 'F방'이라면 에피소드는 종료, 그렇지 않은 경우는 이동 목적지를 현재의 방으로 합니다.
5. 위 2번에서 다시 반복합니다.
에피소드 1
그럼 ⑥단계에 따라, 에피소드 1의 시뮬레이션을 실시해봅시다.
1. 랜덤으로 초기 상태를 선택합니다.
이번에는 방 C를 초기 상태로 합니다.
2. 현재 상태에서 이동할 수 있는 액션 중 하나를 선택합니다.
C에서 이동할 수 있는 방은 B 또는 F입니다.
이번에는 이 중에서 F를 선택했다고 합시다.
3. Q계산식에 따라 Q값을 계산하여 Q보드에 씁니다.
F에서 이동 가능한 액션은 C, E, F의 3가지입니다.
Q계산식에 적용시켜 보면 다음과 같습니다.
Q (C, F) = R (C, F) + 0.8 × Max (Q (F, C), Q ( F , E ), Q (F, F))
아직 처음이므로 Q보드는 그림 4Q처럼 모두 0으로 되어있습니다.
즉 Q (F, C) 도 Q (F, E) 도 Q (F, F) 도 값이 0이므로 Max (Q (F, C), Q (F, E), Q (F, F))는 0입니다.
그림 4R을 보면 R (C, F)는 100이기 때문에,
Q (C, F) = R (C, F) + 0.8 × Max (Q (F, C), Q (F, E), Q (F, F))
Q (C, F) = 100 + 0.8 × Max ( 0 , 0 , 0 ) = 100 이 되고,
이 값을 Q보드에 쓰면 아래의 그림 6Q와 같이 됩니다.
4. 이동한 곳이 F라면 종료, 그렇지 않다면 이동 공간을 현재 객실로 합니다.
이번에는 F이므로 에피소드 1이 완료됩니다.
에피소드 2
이어 에피소드 2입니다.
1. 랜덤으로 초기 상태를 선택합니다.
이번에는 B를 초기 상태로 합니다.
2. 현재 상태에서 이동할 수 있는 액션 중 하나를 선택합니다.
B에서 이동할 수 있는 방은 A, C, E입니다.
이번에는 이 중에서 C를 선택합니다.
3. Q계산식에 따라 Q값을 계산하여 Q보드에 씁니다.
C에서 가능한 액션은 B와 F입니다.
Q계산식에 적용시켜 보면 다음과 같습니다.
Q (B, C) = R (B, C) + 0.8 × Max (Q (C, B), Q (C, F))
그림 6Q에 따르면, Q (C, B)는 0에서 Q (C, F )가 100이므로
Q ( B , C ) = 0 + 0.8 × Max ( 0 , 100 ) = 80이 되고,
이 값을 Q 보드에 쓰면 아래의 그림 7Q와 같이 됩니다.
4. 이동한 곳이 F라면 종료, 그렇지 않다면 이동 공간을 현재 객실로 합니다.
이번에는 F가 아닌 C이므로, 다시 2에서 시작합니다.


에피소드 2에 이어서 계속
2. 현재 상태에서 이동할 수 있는 액션 중 하나를 선택합니다.
C에서 이동할 수 있는 방은 B 또는 F입니다.
이번에는 운 좋게 F를 선택했다고 합시다.
3. Q계산식에 따라 Q값을 계산하여 Q보드에 씁니다.
F에서 가능한 액션은 C, E, F의 3가지입니다.
Q계산식에 적용시켜 보면 다음과 같습니다.
Q (C, F) = R (C, F) + 0.8 × Max (Q (F, C), Q ( F , E ), Q (F, F))
그림 7Q를 참조하면 Q (F, C) 도 Q (F, E) 도 Q (F, F) 도 값이 0이므로,
Max (Q (F, C), Q (F, E), Q (F, F))은 0입니다.
그림 4R을 보면 R (C, F)는 100으로 되어있기 때문에,
Q (C, F) = R (C, F) + 0.8 × Max (Q (F, C), Q (F, E), Q (F, F))
Q (C, F) = 100 + 0.8 × Max ( 0 , 0 , 0 ) = 100
이미 Q (C, F) = 100 이므로 , 이번은 Q보드의 값을 변화시키지 않습니다.
4. 이동한 곳이 F라면 종료, 그렇지 않다면 이동 공간을 현재 객실로 합니다.
이번에는 F이므로 에피소드 2는 종료입니다.
에피소드 n
에피소드(경험)를 쌓아가면서 Q보드에 값이 차례로 입력되고, 전략 보드로서의 역할을 하게 됩니다.
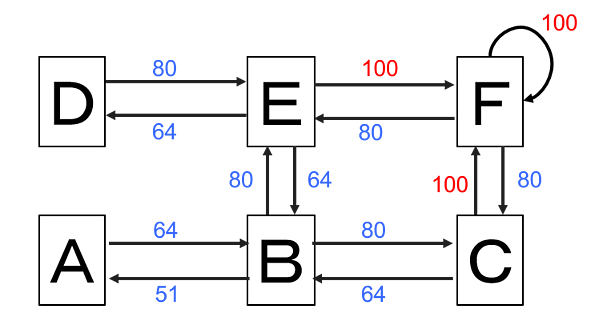
이번에는 간단한 모델이므로, 에피소드를 반복해 과는 과정에서 결국 Q보드는 그림 8Q와 같이 됩니다.

그림 8Q의 값을 백분율로 나타내 봅시다. 최대 값 500으로 나누면 그림 9Q처럼 나타낼 수 있습니다.
이 정보를 그림 3의 흐름에 적용하면 그림 10과 같이 됩니다. 학습을 통해 이 같은 정보를 얻을 수 있다면, 에이전트가 A방에 있었다고 해도 최단 경로로 영희가 있는 F방에 도착할 것입니다.

강화 학습이란?
자 그럼, 튜토리얼을 통해 강화 학습의 이미지를 잡을 수 있었지요? 강화 학습은 그림 11과 같이 어느 환경에서 에이전트의 현재 상태에서 행동한 결과로 주어지는 보상을 극대화하기 위해 에피소드를 반복해 가는 학습법입니다. 위의 튜토리얼에서 환경은 6개의 방이고, 상태는 지금 있는 방, 행동은 방을 이동하는 것, 그리고 보상은 영희를 만나는 것입니다.
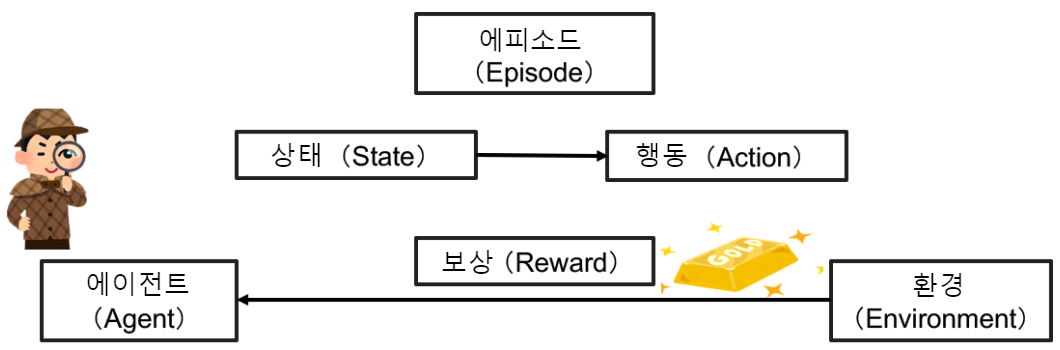
그림 11의 관계를 '장기'에 적용해 보면 어떻게 될까요. 먼저 환경은 장기이고 에이전트는 나 자신이네요. 그리고 최대의 가치(보상)는 장기에서 승리하는 것입니다. 지금 상태에서 다음 수(행동)를 두는데, 눈앞의 이익(즉시 보상)에 집착하면 악(惡)수를 두게 됩니다. 어디까지나 마지막에 승리(미래 가치)를 극대화하기 위한 수를 두어야 합니다. 그 이정표를 얻기 위해 자신과 스스로 수백만 번 맞붙어 에피소드마다 결과를 정성껏 Q보드에 저장해 가는 것입니다.
강화 학습은 즉각적인 보상(Immediate rewards : 즉시 보상) 대신 미래에 얻을 수 있는 가치를 극대화시킬 수 있도록 행동합니다. 따라서 "어떤 상태에서 한 행동을 취했을 때의 가치"를 탐험(에피소드)을 통해 찾아갑니다. 이 가치를 Q값(상태 행동 가치)이라 하며 얻어진 정보(가치의 기대치)를 Q보드에 저장하여 둡니다. Q값은 Q(sa)라는 함수로 표현되며, s는 상태 a는 액션입니다. 예를 들어, 그림 9Q에서 Q (E, D)은 64라는 기댓값이 기록되어 있습니다.
|
DQN과 Rainbow 강화 학습을 공부하다 보면 DQN이라는 말이 자주 나옵니다. 이것은 Deep Q-Network라는 Google(DeepMind사)가 개발한 인공 지능 딥러닝(CNN) 기술을 사용하여 Q학습(Q-Learning)을 하는 것입니다. 2015년에 등장해 "처음부터 게임을 통해 자력으로 공략법을 찾는 인공지능"으로 각광받고, AlphaGo에 도입되어 그 위력을 알리고, 강화 학습의 급속한 붐을 일으킨 업체가 되었습니다. 그 후, 다양한 개량이 더해져 현재는 Rainbow라는 새로운 알고리즘이 탄생하였습니다. |
강화 학습 알고리즘
강화 학습에는 몇 가지 알고리즘이 있습니다. 여기에서는 그림 12의 Q-Learning(Q학습), Sarsa(살사), 몬테카를로에 대해 간단하게 알아봅시다.

(1) Q-Learning
위의 '영희 구출 미션'에서는 기대치 Q를 찾는데 식 1과 같이 계산을 했습니다.
Q(상태, 액션) = R(상태, 동작) + γ × Max(Q (다음 상태 모든 액션))... (식 1)
이에 α라는 매개변수를 추가하면 식 2가 되고, 이것이 Q-Learning의 기본적인 계산식입니다.
Q(상태, 액션) = (1-α) Q(상태, 동작) + α( R (상태, 액션 + γ × Max(Q ( 다음 상태 모든 조치 )))... (식 2)
α는 학습률이라 불리며 Q값 경신의 완급을 결정하는 파라미터입니다. 이 식을 간단하게 작성하면 다음과 같습니다.
Q (현재 값) = (1-α) Q ( 현재 값 ) + α Q ( 새로운 값 )
α는 0에 가까울수록 완만하게, 1에 가까울수록 급격하게, 새로운 Q 값을 반영합니다. 식 1에서 α=1로 1 항목을 생략하고 가장 급격히 Q값을 경신하였던 것입니다.
(2) Sarsa
Sarsa(살사)의 계산식은 식 2에서 Max함수를 걷어내어 식 3이 됩니다.
Q ( 상태, 액션 ) = (1-α) Q ( 상태, 동작 ) + α (R ( 상태, 동작 ) + γ Q ( 다음 상태, 모든 액션 ))... (식 3)
Q-Learning은 다음의 상태에서 취할 수 있는(이동 가능한) 선택의 최대 기대치를 새로운 Q값으로 했지만, Sarsa는 실제로 하나씩 행동한 결과로 Q값을 경신합니다.
(3) 몬테카를로
몬테카를로 법은 이전에 '랜덤으로 시도하여 그 결과의 근사치를 구하는 시뮬레이션 법'이라고 간략하게 설명을 했었습니다만, AlphaGo가 '바둑알을 움직이는 방법'의 평가에 사용하는 중요한 기술이므로, 위의 두 방식과의 차이점과 함께 좀 더 자세히 알아봅니다.
몬테카를로 법도 Q값(전략 보드)을 갱신해 나가는 것은 동일하지만 위의 두 경우와는 달리, '다음 상태의 Q값'을 사용하지 않습니다. 대신 보상 배열을 제공합니다.
① 어쨌든 보상을 얻을 때까지 행동합니다.(그림 2의 예라면 F방에 도달할 때까지 계속 이동)
② 거기에 이르기까지의 액션과 얻은 보상을 보상 배열에 모두 기록합니다.
③ 보상에 도달하면, 그때까지 기록된 배열의 평균치로 Q값을 식 4로 업데이트합니다.
Q ( 상태, 액션 ) = Ave (배열 ( 상태 작업 ))... (식 4)
몬테카를로 법은 각 작업에서 Q값을 경신하는 위 두 방법과 달리 보상에 도달한 시점에 도달할 때까지 얻은 가치(배열에 저장된 정보)를 사용하여 단숨에 Q값을 경신합니다. '성과를 내지 않으면, 당신이 평소 어떤 일을 했는지 평가할 수 없다'라는 성과주의의 화신과 같은 악마 상사라 할 수 있겠습니다.
상태 행동 공간의 폭발
영희 구출 미션에서는 상태와 동작의 매트릭스(Q보드)가 작기 때문에 Q값도 제한된 숫자로 끝났습니다. 그러나 이 방법을 그대로 바둑에 적용하려 하면 그리 쉽지가 않습니다. 바둑은 칸이 19 × 19로 아주 크기 때문에 몇수만 다르게 둬도 "이것은 예전에 본 적 없는 국면이네요"라고 해설자가 설명합니다. 그래서 "어느 국면에서의 다음 수"라는 조합이 너무도 방대하여 Q보드에 저장할 Q값이 무한대가 되어 버립니다. 이러한 문제를 상태 행동 공간의 폭발(The state and action space explosion ploblem)이라고 합니다.
이 문제를 해결하기 위해 Q값을 직접 구하는 대신 함수로 근사 시키는 방법을 생각할 수 있습니다. 어느 정도 Q값을 취득한 곳에서 비선형 함수로 근사하고, 모든 Q값을 구하지 않아도 함수로 Q값을 추정할 수 있도록 하는 것입니다(이전의 회귀 곡선을 떠올려 주세요). 그리고 이 함수 근사 신경망 기술을 적용하여 근사 정밀도를 향상한 것이 DQN입니다.
정리
그럼, 강화 학습의 구조가 해전 게임과 같이, 어떻게 전략 보드의 Q값을 얻어 나가는지 아시겠지요?. 강화 학습은 장기나 바둑 등에서 인간을 초월할 수 있음을 입증하고 있으며, 금융 거래에서도 그 위력을 발휘하고 있습니다. 앞으로의 발전이 기대되며, 조금 SF적인 불안감도 느껴지게 하는 기술이네요.
'AI · 인공지능 > 알기쉬운 AI' 카테고리의 다른 글
| [알기쉬운 AI - 28] CNN(Convolutional neural network) (0) | 2020.05.17 |
|---|---|
| [알기쉬운 AI - 27] 클러스터링 (Clustering) (0) | 2020.05.07 |
| [알기쉬운 AI - 26] 분류 (Classification) (0) | 2020.04.26 |
| [알기쉬운 AI - 25] 회귀 (Regression) (0) | 2020.04.25 |
| [알기쉬운 AI - 23] P 값과 Q 값 (3) | 2020.03.25 |
| [알기쉬운 AI - 22] 강화학습과 도적 알고리즘 (1) | 2020.03.18 |
| [알기쉬운 AI - 21] 과학습을 막는 방법 (0) | 2020.03.14 |
| [알기쉬운 AI - 20] 비정상적인 과학습 (0) | 2020.02.10 |



