
시작하기
CNN, RNN, LSTM 등 3회에 걸쳐 딥러닝을 지원하는 대표적인 알고리즘을 알아봤습니다. 이번에는 적대적 생성 네트워크 GAN과 DCGAN을 소개합니다. 지금까지 봤던 식별과 회귀 등의 인공지능과는 달리, GAN은 생성하는 모델입니다. 딥 페이크 등으로 인해 약간 불명예스러운 낙인이 찍혀있지만, 사람도 아티스트가 좋은 것과 기술을 배워가며 자신의 작품을 만들어 가듯이 GAN도 이미 훌륭한 크리에이터로서의 품격을 내비치고 있습니다.
GAN이란?
GAN(Generative Adversarial Networks)은 2개의 네트워크가 절차탁마하면서 서로 성장해가는 비지도 학습 모델입니다. 부모가 가르치지도 않았는데, 두 형제가 끊임없이 장기와 바둑을 두는 사이에 부모보다 훨씬 강해지는 것. 이것이 바로 GAN형제입니다. 이 둘은 각자의 역할이 있으며, 형 generator는 가짜 생성기이고, 동생 discriminator는 그것을 간파하는 역할입니다. 이 관계에서 적대적(Adversarial)이라는 말이 붙었습니다만, 실제로는 착한 동생이 형의 성장을 위해 협력하는 이미지입니다(GAN의 주역은 형인 '생성기'입니다).
그림 1, GAN의 기본 구조를 참조하십시오. 형이 실물의 샘플을 모방한 가짜를 만들어서, 진짜와 가짜를 교대로 동생에게 보여줍니다. 동생은 가짜를 봤을 때, 어느 쪽의 확률이 높은지 판단하여, 시그모이드 함수(RNN때 나았었죠)에 의해 사실(1)인지 가짜(0)인지 구별합니다. 그리고 동생이 정답 여부를 판정할 때, 오차 역전파(Backpropagation)에 의해 형과 동생을 차례로 훈련(가중치 변경)시킵니다. 일반적으로 훈련은 미니 배치 1세트씩 번갈아가며 수행하며, 형이 훈련할 때는 동생을 고정하고 동생이 훈련할 때는 형을 고정합니다.
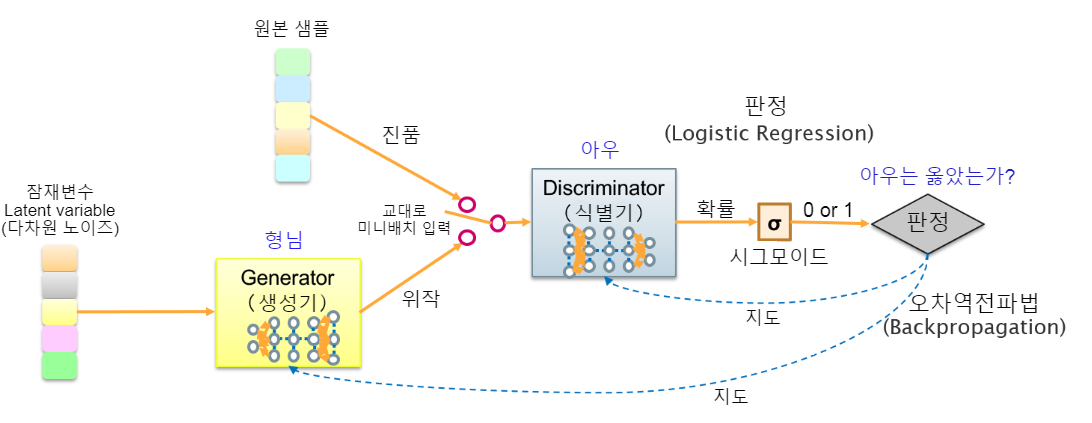
이 훈련을 통해 형은 더욱 모방을 잘할 수 있게 되고, 동생도 뭐든 감정 가능한 수준으로 성장합니다. 결국, 형이 "위작의 명인"이 되어 현실과 전혀 구분할 수 없는 가짜를 생성할 수 있게 되면, 동생의 판정 확률이 반반이 되면서 미션이 종료됩니다.
실제로 GAN에서 무엇을 할 수 있는지 아래 YouTube 동영상을 보세요. 영상 1은 왼쪽의 남성과 똑같이 동작하는 여자의 모습입니다(후반은 남녀의 역할이 바뀌고 있습니다). 이 현실감 있는 미녀는 사실, 실물을 샘플로 하여 GAN으로 학습하여 만들어낸 가짜입니다.
GAN은 이러한 학습 기법의 총칭으로 다양한 베리에이션이 있습니다. 영상 1은 그중에 하나인 Cycle GAN을 사용하여 학습하고 있습니다. 이번에는 이미지 생성을 크게 발전시킨 CNN을 이용한 DCGAN을 알아보겠습니다.
잠재 변수와 노이즈
여기서 이러한 의문이 떠오릅니다.
"우선 잠재 변수란 무엇인가?
형인 generator는 무엇을 바탕으로 가짜를 만들고 있는가?"
이에 답하려면 통계 이야기를 먼저 하지 않으면 안 됩니다.
(1) 생성과 인식
먼저 알아둘 것은 생성과 인식은 대칭 프로세스라는 것입니다. 그림 2와 같이 독말풀 이미지의 특징점을 인식하고 변수화 할 수 있다면, 그 반대로 특징점(n차원의 잠재적 변수)에서 이미지를 생성할 수 있어야 합니다. 이것이 생성 모델의 기본 개념입니다.

(2) 잠재 변수와 관측 변수
세상에는 직접 측정하기 어려운 추상적인 척도가 많습니다. 예를 들어, 영희를 좋아하는 마음은 정작 자기 자신의 마음이지만 잘 표현할 수 없습니다. 도대체 사람을 좋아하는 정도를 어떻게 측정하면 좋은 것일까요. 고민 끝에 다음의 세 가지 요소로 질문을 작성하여 5단계 평가로 답변하기로 했습니다. 3개 답변의 합계로 사랑의 정도를 점수화하는 것입니다.
1. 영희를 생각...> 일주일에 몇 번 생각하는가?
2. 영희가 보고 싶다...> 일주일에 몇 번 보고 싶은가?
3. 이 경치를 영희에게 보여주고 싶다...> 좋은 경치를 볼 때 어느 정도의 확률로 영희가 생각나는가?
이 경우 직접 측정할 수 없는 "좋아하는 정도"를 잠재 변수라 하고, 몇 회 라든지 확률이라든지 수치화가 가능한 요소를 '관측 변수'라고 합니다. 사실 잠재 변수의 개념은 지금까지의 학습에서도 나왔습니다. 서포트 벡터 머신(SVM)에서 (행동적/신중함, 사교적/내성적)등의 성격 테스트를 통하여 이를 관측 변수로 영업 성향인지 관리 성향인지 잠재적 변수를 결정했었지요.
또한 '클러스터링'에서는 고객의 특성(잠재 변수)을 상점에서 구입한 횟수나 인터넷에서 구입한 횟수를 관측 변수로 그룹화하였고, 차원 감소에서 나온 주성분 분석(PCA)에서도 무게, 내압, 탄력, 딱딱함, 촉감이라는 5개의 관측 변수를 바탕으로 '푹신도'와 '매끈도'라는 잠재 변수를 찾고 있었던 것입니다.
(3) 생성 모델(generative model)과 식별 모델(discriminative model)
생성 모델과 식별 모델의 차이점을 자세히 살펴보겠습니다. 생성 모델은 데이터의 분포 상태를 확률적으로 파악하고, 그 분포 법칙에 따라 데이터를 생성하는 확률 모델입니다. 한편, 식별 모델은 확률을 사용하지 않습니다. 주어진 데이터를 SVM과 k균형법, CNN 등에 의해 식별하는 모델입니다.
같은 인식 모델도 SVM처럼 단순히 경계면만을 학습하는 유형과 k균형법이나 k평균법과 같이 데이터 분포를 학습하는 유형이 있습니다. 그리고 데이터 분포를 인식하고 있다면, 식별의 역과정으로 분포의 한가운데(확률적으로 여기가 제일이라는 포인트)에서 데이터를 생성할 수 있습니다. k평균법으로 새로운 중심을 찾고 있던 것은 바로 한가운데를 찾고 있던 것입니다.
SVM : 데이터 군을 가장 잘 분해한다. 강폭을 최대로 하는 경계를 찾기.
k 균형법 : 근처에 많이 있는 그룹으로 구분. 다수결로 분류한다.
k 평균법 : 1. 그룹마다 중심을 찾고,
2. 가장 가까운 것이 새로운 중심 그룹이 된다.
이것을 반복하는 방법.
(4) 동시 확률 분포
확률 모델에는 동시 확률 분포라는 개념이 있습니다. 피자 가게의 예로 살펴보겠습니다. 파*존* 피자의 회원 1000명 중 1개월 이내에 신상품 "찐파*스 피자(가칭)의 할인 쿠폰"을 취득한 사람과 피자를 주문한 사람을 집계해 보면 표 1과 같습니다.
| 그룹 | 쿠폰 검색 X | 피자 구매 Z | 인원 | 결합 분포 p ( X, Z ) |
| 쿠폰으로 구매 | ○ | ○ | 200 | p ( 1,1 ) = 0.20 |
| 쿠폰만 받음 | ○ | × | 250 | p ( 1,0 ) = 0.25 |
| 쿠폰 없이 구매 | × | ○ | 150 | p ( 0,1 ) = 0.15 |
| 쿠폰도 구매도 없음 | × | × | 400 | p ( 0,0 ) = 0.40 |
| 합계 (확률 분포) | p (X) = 0.45 | p ( Z ) = 0.35 | 1000 | 1 |
표 1 : 회원 1000명의 1개월치 CRM 정보
쿠폰 보유자를 X, 피자 구매자를 Z라고 하자(X와 Z는 확률 변수).
X와 Z가 서로 간에 영향을 무시하고 별도의 확률 분포(주변 확률)를 요청하고
쿠폰을 취득한 사람의 주변 확률 p(X)는 0.45,
피자를 구입한 사람의 주변 확률 p(Z)는 0.35입니다.
서로 영향을 고려한 경우(동시 확률 분포)는 2개의 확률 변수를 사용하여 p(X, Z)로 나타냅니다. 두 변수가 모두 변화하면 계산하기 어렵기 때문에 하나를 고정하고, 다른 하나의 변화로 살펴보겠습니다(조건부 확률 분포).
※확률의 덧셈 정리와 곱셈 정리
○ 통계는 어찌해도 수식이 나와 버리기 때문에, 용어와 기호를 복습하고 가겠습니다.
- X와 Z : 확률 변수
- 주변 확률 : p(X)
- 동시 확률 분포 : p(X, Z)
- 조건부 확률 분포 : p(Z | X) ... X가 일어나는 조건에서 Z의 확률
○ 하는 김에 다음 두 가지 정리도 기억할까요?
- 확률의 덧셈 정리 : p(X) = ΣZp(X, Z)
- 확률의 곱셈 정리 : p(X, Z) = p(Z | X) * p(X)
○ 예를 들어 표 1에 적용시켜 보면 다음과 같이 정리가 성립되는 것을 알 수 있습니다.
- 덧셈 정리 : p(1) = ΣZp (1, Z) ⇒ 0.45 = 0.25 + 0.20
- 곱셈 정리 : p(1,1) = p(1,1) / (p(1,1) + P(1,0)) * p(1) ⇒ 0.2 = 0,2 / (0.2 + 0.25) * 0.45
그럼, X를 고정하고 Z의 변화를 지켜보는 조건부 확률 p(Z | X)를 살펴봅시다. 쿠폰을 받은(X=1) 사람을 대상으로 피자를 구입한 사람(Z=1)의 확률을 구하면, 쿠폰을 받아서 구매 p(1,1) = 0.2명, 쿠폰만 받은 사람 p(1,0) = 250명이므로 0.2 / (0.2 + 0.25) = 0.44입니다. 또 쿠폰이 없는 사람 (X=0)을 대상으로 피자를 구입한 사람(Z=1)의 확률은 0.15 / (0.15 + 0.4) = 0.27로 쿠폰을 취득한 사람에 비하면 60% 정도가 된다는 것을 알 수 있습니다.

(5) 생성적 확률 모델과 잠재 변수 모델
앞서 설명한 바와 같이 데이터의 확률 분포에 기초하여 데이터를 생성하는 생성적 확률 모델입니다. 잠재 변수 모델은 생성적 확률 모델이며, 관측 변수 X와 잠재 변수 Z와 파라미터 θ를 갖습니다. 이 잠재 변수 모델을 p(x, z | θ)로 작성합니다. 관측 변수 X는 측정 가능하지만, 잠재적 변수 Z와 매개 변수 θ는 알 수 없는 변수입니다. 2개의 미지의 값이 있기 때문에 조건부 확률 분포로 비교해 잠재 변수 Z를 고정하여 θ를 구하고, 다음 θ를 고정하여 잠재적 변수 Z를 구하는 것입니다.
여기까지 이해한 후에 다시 한번 그림 1을 참조하십시오. 형 generator는 잠재 변수 모델 생성기이므로 p(x, z | θ)로 표시됩니다. X가 관측 함수이고 Z가 잠재 변수입니다. θ는 무엇일까요? 이것은 데이터 분포의 우도를 최대화하는 파라미터입니다. 우도는 '[26] 분류'에서 나왔던 '가장'을 의미하는 확률로 likelihood 였지요. 음... 동생 discriminator가 간파함으로써 오차 역전파로 조정되는 형의 가중치(필터)로, "데이터 분포의 한가운데"를 결정하는 파라미터가 된다고 이해하세요.
생성하는 잠재 변수(데이터 분포의 중간)를 변경하는 경우에는 형의 가중치를 갱신하지 않고(θ를 고정) 학습합니다. 그리고 형의 조교의 경우는 잠재 변수 Z를 고정(던지는 공을 일정하게)하여 θ에 가중치를 갱신하는 처리를 교대로 실시하고 있는 것입니다.
DCGAN
여기에서 다시 생성 모델을 돌아봅시다. 아무것도 없으면 이미지가 생성되기 어렵기 때문에, 이미지에서 이미지를 생성하는 이미지 변환을 소재로 합니다. 그림 4는 모네의 화풍을 흉내 내는 훈련을 한 형이 사진을 바탕으로 모네의 터치로 그림을 생성한 예입니다. 이웃집 고흐와 비교하면 대단히 모네 같네요. 언어 번역의 사진판이라는 것으로, 화상 번역이라고도 하는 기술입니다.

이러한 이미지 처리는 CNN의 십팔번입니다. 따라서 CNN을 이용한 DCGAN(Deep Convolutional Generative Adversarial Networks)이 나타나면서 GAN의 이미지 생성 기술을 비약적으로 향상했습니다. Deep Convolutional이라고 말 그대로 심층 콘볼루션이라는 말이므로, 조금 안이하게 느껴지는 네이밍입니다.
사실 그림 1의 형과 아우도 NN의 이미지를 갖고 있었습니다. 이것도 DCGAN이었습니다. 그리고 형의 NN이 아우와는 역방향이라는 것을 눈치챈 사람은 '틀린 그림 찾기 대회'에 출전할 자격이 있을지도 모릅니다. 이것은 실수로 그런 것이 아니거든요.
먼저도 말했듯이 생성 모델(generative model)은 인식 모델( discriminative model)과 반대의 일을 합니다. [28]에서 배운 콘볼루션 신경망(CNN)을 사용하여 입력된 이미지가 모네의 그림인지 여부를 판정합니다. 이것이 동생의 역할입니다. 콘볼루션 처리 및 풀링 처리를 반복하여 큰 이미지를 작은 여러 개의 이미지로 변환하는 것, 마지막으로 전 결합층의 다수결로 결정하는 것이었지요.
그러나 DCGAN의 동생은 풀링층을 보폭 2회선 (1픽셀씩이 아니라 2픽셀 간격으로 콘볼루션 처리 = 보폭 1보다 작은 수)로 대체하거나, 전 결합층에서 전체 경우의 수대로 대입하는 대신 global average pooling(출력 이미지마다 화소 평균값을 구하여 그것을 1대 1로 출력 = 출력에 연관된 가중치 파라미터가 크게 감소)등 처리의 경량화를 실시하고 있습니다(그림 5).
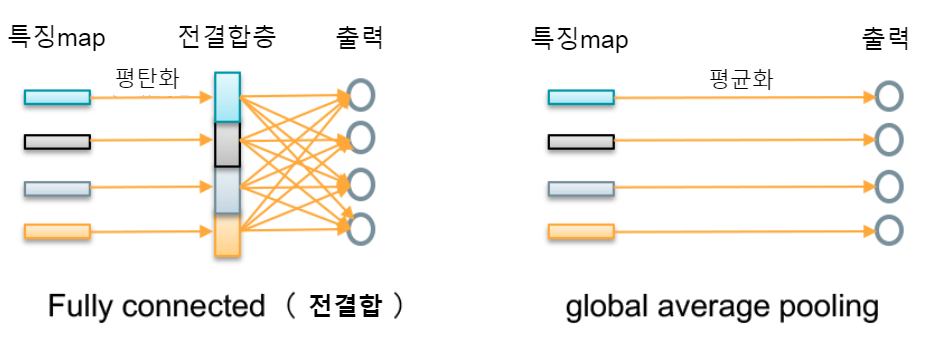
한편, 형은 콘볼루션 처리의 반대의 일을 합니다. n차원의 잠재 변수를 종으로 하여, 역 콘볼루션 처리(deconvolution)를 실시하여, 씨앗에서 시작하여 서서히 모네 같은 그림으로 성장시켜서 마지막에 1장의 그림을 완성해내는 것입니다. 동생은 업 샘플링하는 역방향 콘볼루션 신경망입니다(그림 6).

GAN 학습
GAN의 씨앗으로는 균일한 분포와 정규 분포를 바탕으로 구한 잠재 변수를 사용합니다. k평균 법의 초기 배분이 인간이 느끼기에 이상했던 것과 같네요. k평균 법은 거기에서 EM 알고리즘을 반복하면서 수렴했습니다. DCGAN도 마찬가지입니다. 학습 초기형의 출력은 아날로그 TV의 모래폭풍 화면(아, 젊은이들은 잘 모를지도...)과 같이, 노이즈 일색이라는 느낌입니다.
GAN은 비지도 학습이기 때문에, 학습에 시간이 걸리고 제대로 임무를 완성시키기 어렵습니다. 학습은 실제 데이터 량 (사진 매수)과 잠재 변수의 차수가 포함됩니다. 데이터 량과 차원이 많을수록 정확도가 높은 것을 만들어낼 수 있지만 차원을 100, 200으로 늘려갈수록 그만큼 학습에 시간이 걸립니다. 아무래도 씨앗이 랜덤 노이즈의 뿐이라면 학습이 매우 힘들기 때문에 Conditional GAN 등 데이터의 일부에 라벨을 붙인 반 감독 학습 모델이 등장했습니다. 반 감독 학습 내용은 다음에 정리해서 설명하겠습니다.
GAN의 학습에는 '[17] 기계학습 방법'에서 배운 미니 배치 학습법(원래의 데이터에서 무작위로 소량을 뽑아내어 배치 학습하는 것을 여러 번 반복)이 사용됩니다. 학습은 야구와 미식축구 같은 교대제로 정품만을 학습한 후 가짜만으로 학습하는 일괄 학습을 교대로 실시합니다. 형 generator는 순진하기 때문에, '[22] 강화 학습과 도적 알고리즘'에서 나왔던 영희와의 가위 바위 보처럼, '한쪽이 계속 이어졌기 때문에 다음에도 그쪽일 것이다'라는 베이즈 확률론(Bayesian probability)은 잘 알지 못합니다.
형의 학습에는(동생도 사용할 수 있습니다), Batch Normalization(배치 정규화)가 사용됩니다. 이것은 신경망 각층의 출력 데이터를 표준화 함으로써 경사 소실 · 폭발 및 과학습을 방지하는 궁리입니다. 또한 형의 활성화 함수 (입력 신호의 총합을 출력 신호로 변환하는 전달 함수)는 출력 계층만 Tanh을 사용하지만, 그 이외의 층은 ReLu라는 램프 함수를 사용합니다. 한편, 동생은 모든 계층에서 Leaky ReLU를 사용합니다. ReLu는 x가 음수이면 0을, 양수이면 입력 값 x를 출력하는 함수이고, Leaky ReLU는 x가 음수이면 0.2x를, 양수이면 입력값 x를 출력하는 함수입니다(그림 7). 왜 이러한 함수를 사용하는지 설명하자면 복잡한 수식이 많이 나오기 때문에 여기서는 생략하겠습니다.
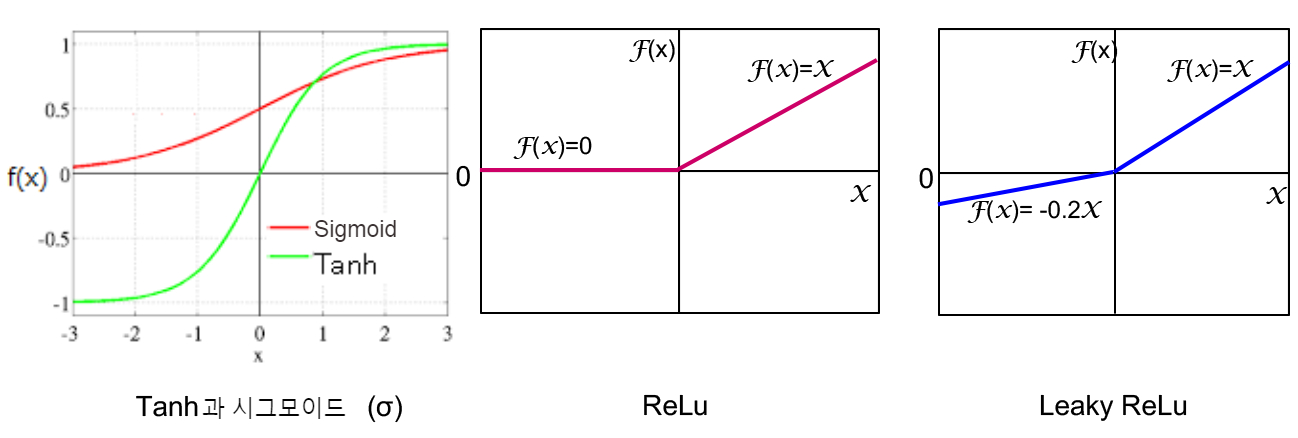
학습 데이터를 1 순회하면 1 epoch로 계산됩니다. epoch마다 동생과 형의 손실 비율(얼마나 잘못했는지)이 표시되기 때문에, 우리는 이러한 값을 확인하면서 훈련을 진행합니다. 이 둘은 균형 있게 성장해야 합니다. GAN의 독특한 점은, 형이 진짜를 본 적이 없다는 것입니다. 정품을 그대로 모방하는 것이 아니라 실제 같은 특징을 잡고, "이봐, 이런 특징이 있으면 진짜라고 생각해"라는 식으로 동생(그는 언제나 진짜도 보고 있습니다)만 속일 수 있으면 됩니다.
따라서 동생이 너무 약한 경우, 형은 상대의 약점을 틈타서 같은 카드를 계속 내버립니다. 반대로 동생이 너무 강해서 무엇을 내놓아도 간파당해 버리면 형은 경사 소멸이라는 깊은 미로 속으로 들어가 버립니다. 또한 학습마다 강약을 조절해 가면서 진폭의 흐름을 타기 쉬워 생성물의 결과가 좋아졌다가 나빠졌다가 합니다. 진폭을 하면서도 수렴하면 좋겠지만, 그대로인 경우도 많습니다.
업샘플링
"CNN은 정보량을 줄이는 거니까 그렇다고 쳐도, 생성 모델은 그 반대로 적은 정보량에서 풍부한 이미지 따위를 만들 수가 있어요?"
아, 다음은 그 부분입니다. 확실히 jpeg는 엔코더에 의해 이미지를 압축하여 저장할 수 있지만, 디코더로 복원하려 하면 정보가 부족하여 깨진 화면이 됩니다(그림 8). 특징점을 유지하면서 화질도 그대로 작게는 가능하지만, 작은 것에 정보를 더하지 않으면 큰 것은 만들 수 없습니다. 어떤 정보를 더해야 할지 신만이 알 것 같아 보이는데, 업 샘플링은 어떻게 하고 있는 것일까요?

GAN은 신은 아니지만 확률을 사용합니다. '[28] CNN'에서 콘볼루션 연산의 설명에서 3 × 3의 9화소 픽셀의 평균을 1개로 줄였던 것을 기억하십시오. 사실 역 콘볼루션 처리에서도 그 기술을 사용하여 누락된 부분에 평균값을 넣어서 업 샘플링합니다(사실 인간도 마찬가지로 무의식적으로 누락된 부분을 보완하여 사물을 인식하고 있습니다).
그림 9를 사용하여 알아봅시다.
① 상대적으로 확대
3 × 3의 9칸을 5 × 5의 25칸으로 확대합니다(상이). 이때, 여유 픽셀이 있을 수 있으므로, 거기에 제로(0)를 패딩해(묻어) 둡니다.
② 틈새를 중간색으로 채우기
5 × 5의 왼쪽 상단부터 9칸씩 범위를 좁혀, 거기에 포함된 정보의 평균치로 5 × 5 픽셀의 값을 결정합니다. 9칸에 포함된 정보는 a와 b의 2개의 면(a + b) / 2, 4개의 면(a + b + c + d ) / 4를 구하고, 그 값으로 틈새를 메워줍니다. 쉽게 말해서 옆에 있는 정보의 중간 색깔로 틈새를 메우는 것입니다. 이것을 왼쪽부터 1픽셀씩 순차적으로 실시하여, 틈새에 정보가 채워지면서, 옆 셀과의 위화감이 사라지는 것입니다.
③ 특징 비교
크기가 업 되었다면, 다음은 CNN과 마찬가지로 필터(특징)를 비교하여 이미지를 변환합니다.

정리
이번에는 지금 가장 주목받고 있는 AI기술의 하나인 GAN을 알아봤습니다. 생성이 주역인 GAN을 발전시키기 위한 연구가 세계적으로 진행되고 있으며, 우리의 생활에 실용화된 것이 속속 등장하고 있습니다. GAN의 발전 역사와 사용 용도에 대해서는 추후 별도의 칼럼으로 정리하겠습니다.
'AI · 인공지능 > 알기쉬운 AI' 카테고리의 다른 글
| [알기쉬운 AI - 35] 설명 가능한 AI(XAI : Explainable AI) 2 - XAI의 적용 방법 (0) | 2023.01.20 |
|---|---|
| [알기쉬운 AI - 34] 설명 가능한 AI(XAI : Explainable AI) 1 - AI의 예측에 근거는 필요한가? (0) | 2022.11.06 |
| [알기쉬운 AI - 33] CNN이란 어떤 것인가? (0) | 2022.10.10 |
| [알기쉬운 AI - 32] 신경망은 만능인가...? (1) | 2021.10.24 |
| [알기쉬운 AI - 30] LSTM (Long Short-Term Memory) (0) | 2020.05.29 |
| [알기쉬운 AI - 29] RNN(Recurrent Neural Network) (1) | 2020.05.23 |
| [알기쉬운 AI - 28] CNN(Convolutional neural network) (0) | 2020.05.17 |
| [알기쉬운 AI - 27] 클러스터링 (Clustering) (0) | 2020.05.07 |



