
신경망은 만능인가...?
AI의 계산방법 중에서도 가장 주목받고 있는 것이 신경망입니다. 그 이유 중 하나로 신경만의 만능성에 있습니다. 이 특성은, 보다 전문적으로는 보편 근사 정리(Universal Approximation Theorem)에 기반에 두는 중요한 특성입니다.
그 보편 근사 정리에 따르면,
유한 개의 유닛을 가지고 1개의 은닉층으로 구성되는 신경망은 특정 조건 하에서 임의의 연속함수를 근사할 수 있다.
여기에서는 그 신경망의 만능성(보편성)을 정성적으로 이해하는 것을 목표로 합니다.
1. 함수로 현상을 나타낸다
함수라는 것은 이를테면 숫자가 들어가고 나가는 상자입니다.

신경망에서는 이 상자의 모양이 자주 보시는 바와 같이 이런 형태를 하고 있습니다.
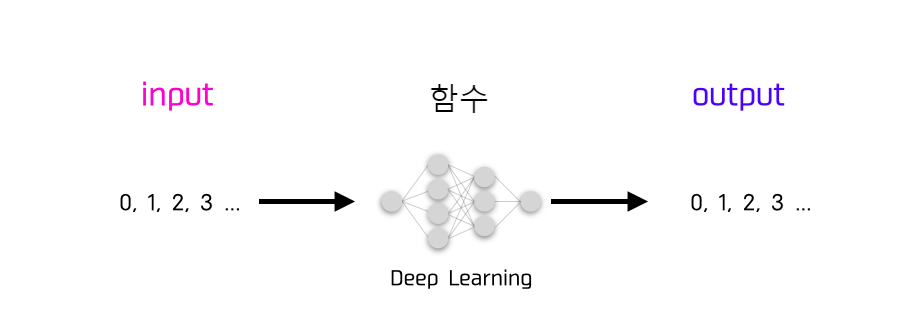
이 인풋과 아웃풋의 숫자로, 이미지의 RGB 정보가 들어가면 이미지 분류가 가능하기도 하고, 음성 데이터가 들어가면 음성 인식이 가능할 것입니다.

이 입력과 출력의 관계를 담당하는 '함수의 형태'를 만드는 것이 곧 '학습한다'라는 것이며, 신경망이 만능이라는 것은, 이 입력과 출력이 어떤 관계일지라도 그것을 나타내는 함수를 만들 수 있다는 것을 의미합니다.
입력과 출력은 숫자이기 때문에 다음 그림과 같은 곡선이 어떤 패턴이라도 대응 가능하다는 것입니다. (여기에서는 편의상 입출력은 1차원이라고 합시다.)

2. 신경망의 계산 절차
그럼, 숨겨진 레이어가 1개 층인 네트워크를 생각해 봅시다.
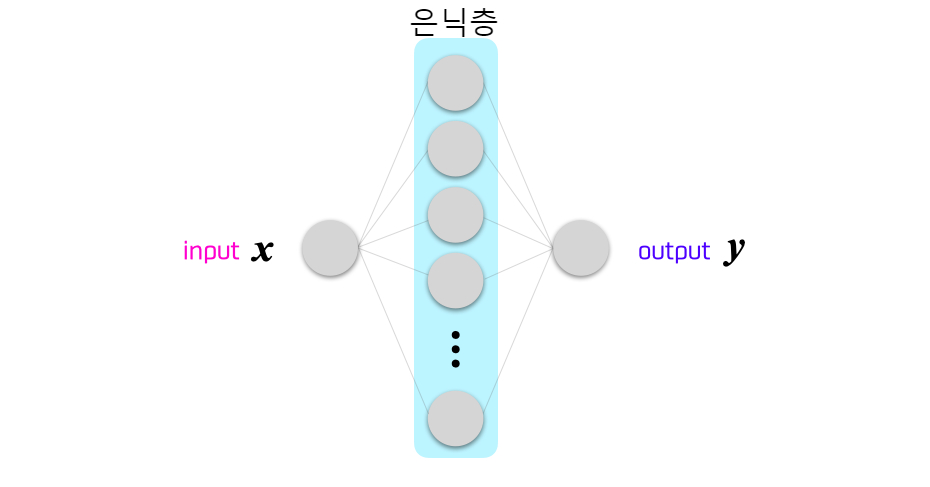
이 계산은 먼저, 입력 숫자에 가중치 w를 곱하고 바이어스 b를 더합니다.
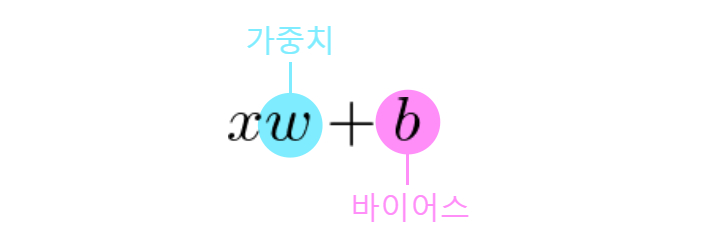
이를 활성화 함수에 넣습니다.
여기에서는 활성화 함수로 이런 형태의 시그모이드 함수라는 녀석을 사용해 보기로 합니다.
(은닉층 이라던지 활성화 함수를 잘 모르겠다 하시는 분은 아래에서 복습하십시오.)
[알기쉬운 AI - 08] AI의 기본 원리
우리 인간은 뇌에서 어떻게 정보를 처리하고 이해하고 있는 걸까요? 현재, 인간은 뇌 속의 수많은 신경 세포(뉴런)가 서로 신호를 전달함으로써 정보를 처리하고 있다는 것을 알고 있습니다. 그
doooob.tistory.com

여기에 아까의 xw + b를 넣어 주면 가중치 w나 바이어스 b의 값을 바꾸는 것으로, 경사라든지 그 위치를 변경시킬 수 있습니다.

그리고 마지막으로, 가중치를 붙여서 더해가는 것으로 은닉층 1층의 신경망 계산은 끝납니다.

3. 임의의 함수를 나타낸다
시그모이드 함수는 가중치 w라든지 바이어스 b의 값을 바꾸면 기울기를 바꿀 수 있다고 했지만, 이해를 돕기 위해 기울기를 완전히 없앤 다음과 같은 스텝 함수를 생각해보기로 합시다.
실제로 이는 가중치를 무한대(∞)로 함으로써 얻을 수 있습니다.

이 스텝의 위치는 가중치 w라든지 바이어스 b의 값을 바꾸면 좌우로 움직일 수 있습니다.
자, 계산 순서에 대해 생각해 봅시다. 입력값 x에 대하여 가중치 w라든지 바이어스 b의 값을 바꾸어 형태가 다른 함수(여기에서는 스텝 함수)를 준비하고 그것을 최종적으로 더해가는 것입니다.
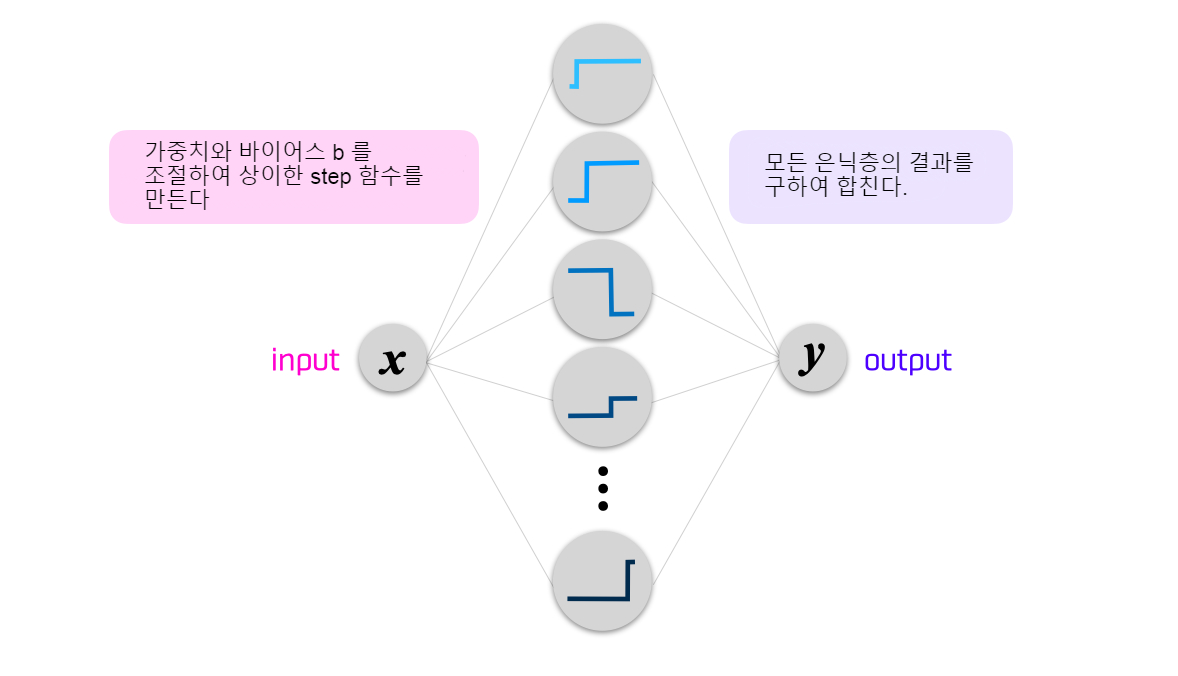
나오는 출력은 예를 들면 이런 느낌이 될 것입니다.
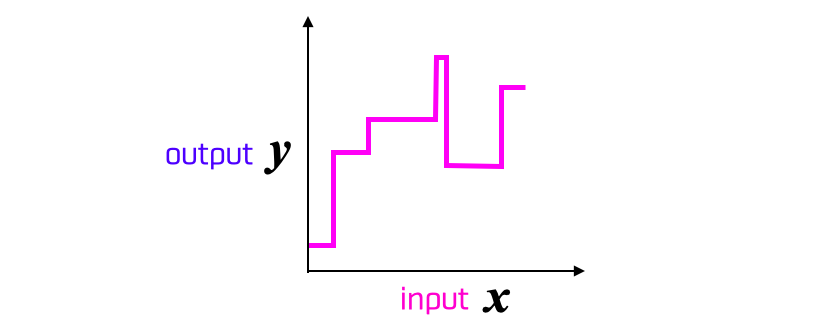
스텝 함수를 사용하고 있기 때문에 각이 지긴 했지만 겨우 함수다워졌습니다. 여기에 은닉층의 유닛의 수를 늘려 보면 어떻게 될까요? 유닛의 수를 늘리는 것은, 더하는 스텝 함수의 수 를 증가시키는 것을 의미하기 때문에 함수의 표현의 폭이 넓어지는 것입니다.

여기까지 오면, 각지긴 했지만, "어떤 모양의 함수든지 표현할 수 있을 것 같다"라는 것을 알게 됩니다.
지금까지는 단순한 스텝 함수에 한정해서 이야기를 했지만, 실제로 신경망에 사용될 수 있는 활성화 함수는 스텝 함수의 각을 깎아내 매끄럽게 한 것과 같은 시그모이드 함수입니다. 이것은 각졌던 이전까지의 함수를 매끄럽게 연결하는 것을 허용합니다.

여기까지 오면, 다음의 보편 근사 정리
유한 개의 유닛을 가지고 1개의 은닉층으로 구성되는 신경망은 특정 조건 하에서 임의의 연속함수를 근사할 수 있다.
가 맞다는 것이 어렴풋이 느껴질 것입니다.
실제로 이 보편 근사 정리는 한ㆍ바나하 정리(Hahn-Banach정리 : 벡터 부분 공간에서 정의된 유계 선형 범함수가 전체 부분 공간으로 확장된다는 함수 해석학의 주요 정리.) 및 리스 표현정리(수학자 리스(Frigyes Riesz)의 이름을 딴 정리로서, 어떤 무한차원 벡터 공간 위에서 정의된 특정 선형 사상을 구체적으로 표현하는 방법을 말해준다. 특히, 힐베르트 공간 위에서 정의된 특정 선형 사상을 내적으로 표현할 수 있음을 알려준다), 푸리에 분석(Fourier analysis)을 사용하여 엄격하게 증명할 수 있다는 것을 알 수 있습니다. 나중에 여력이 되시면 알아보셔도 좋을 것 같습니다.
어떻습니까? AI가 왜 이처럼 범용성이 높은 방법이 되었는지 알 수 있었을까요?
앞으로도 학습 · 연구에 매진하는 가운데, 여러분이 직접 AI를 사용하여 발전시킴으로써 그 응용 범위가 확산되어 진정한 의미의 만능이 되는 것을 바라고 있습니다.
'AI · 인공지능 > 알기쉬운 AI' 카테고리의 다른 글
| [알기쉬운 AI - 36] 설명 가능한 AI(XAI : Explainable AI) 3 - 해석 가능한 모델의 추출 (0) | 2023.02.02 |
|---|---|
| [알기쉬운 AI - 35] 설명 가능한 AI(XAI : Explainable AI) 2 - XAI의 적용 방법 (0) | 2023.01.20 |
| [알기쉬운 AI - 34] 설명 가능한 AI(XAI : Explainable AI) 1 - AI의 예측에 근거는 필요한가? (0) | 2022.11.06 |
| [알기쉬운 AI - 33] CNN이란 어떤 것인가? (0) | 2022.10.10 |
| [알기쉬운 AI - 31] GAN (Generative Adversarial Networks) (3) | 2020.06.07 |
| [알기쉬운 AI - 30] LSTM (Long Short-Term Memory) (0) | 2020.05.29 |
| [알기쉬운 AI - 29] RNN(Recurrent Neural Network) (1) | 2020.05.23 |
| [알기쉬운 AI - 28] CNN(Convolutional neural network) (0) | 2020.05.17 |



