4.1.5. 행렬 곱에 의한 벡터 행렬의 크기 변화
행렬의 전후에서는 행렬의 형태가 변화합니다. 구체적으로는 크기가 (L, M)과 (M, N)인 행렬의 행렬 곱 결과는 크기가 (L, N)인 행렬이 됩니다. 앞의 3개의 연습 문제에서는 행렬과 벡터의 모양과 크기가 어떻게 변화했는지 확인해 봅시다.

특히 (3)에서, 맨 왼쪽의 벡터와 중간 행렬의 곱셈 결과가 행 벡터이기 때문에 크기의 변화가 (1)과 같은 케이스로 귀착된다는 점에 유의하십시오.
또한, 예를 들면 (3,1)의 행렬처럼 차원크기가 1이 된 경우, 그 차원을 삭제할 수 있습니다. 예를 들어 (2)의 계산 결과는 크기가 (2,1) 행렬이지만, 이것은 2차원 벡터로 처리합니다. 마찬가지로, (1), (3)의 결과는 사이즈가 (1,1) 행렬이지만, 스칼라로 간주될 수 있습니다. 이렇게 크기가 1이 된 차원을 찾아서 스칼라 값으로 바꿔 차원을 제거하는 작업을 squeeze라고 부릅니다.
4.1.6. 전치
벡터는 세로로 늘어선 열 벡터를 기본으로 하고 있습니다만, 가로로 늘어선 행 벡터를 사용하고 싶은 경우도 있습니다. 그래서 열 벡터를 행 벡터로, 행 벡터를 열 벡터로 변환하는 작업을 전치(transpose)라고 합니다. 전치 벡터의 오른쪽 어깨에 T로 작성하여 나타냅니다. 예를 들어, x가 3차원 벡터라면,

와 같이 나타냅니다. 전치는 행렬에 대해서도 정의될 수 있습니다. 예를 들어,

이런 식입니다. 행렬에 대한 전치에서는 행과 열이 바뀌기 때문에 크기가 (N, M)이던 행렬이, 전치하면 크기가 (M, N) 행렬이 됩니다. 즉, i행 j열 값이 전치 후에는 j행 i열의 값입니다. 전치 공식으로서 다음을 명심합시다.

전치를 이용하면 두 개의 열 벡터 x, y의 내적 x⋅y는 행렬 곱을 이용하여

로 표기한다는 것에 유의하십시오.
4.1.7. 단위행렬
스칼라 1은 10 × 1=10처럼 임의의 숫자를 1에 곱하여도 값이 변하지 않는 성질을 가지고 있습니다. 행렬의 연산에서 이와 같은 기능을 하는 행렬이 단위행렬 (identity matrix, unit matrix)입니다 (※주석 1). 단위행렬은

와 같은 형태를 하고 있으며, 기호 I 로 나타내는 것이 일반적입니다. 행렬의 사선으로 기울어진 대각선의 요소를 대각(對角) 요소라 하고, 그 이외의 요소를 비 대각 요소라고 부릅니다. 단위행렬은 대각 요소가 모두 1로, 비 대각 요소가 모두 0인 정방 행렬(행과 열 수가 동일한 행렬)입니다. 예를 들어, 2 × 2 단위행렬은

이며, 3 × 3 단위행렬은
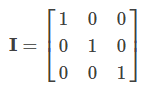
입니다. 행렬의 크기를 명시하고 싶은 경우에는 In ( n × n 단위행렬을 의미)으로 인덱스 크기를 표기할 수 있습니다.
단위행렬은 크기가 동일한 임의의 정방 행렬 A에 대해 다음의 계산이 성립합니다.
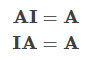
아무 행렬에 단위행렬을 곱해도 원래의 행렬 값이 변하지 않습니다.
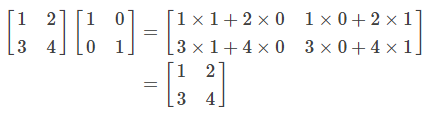
계산 결과에서 알 수 있듯이 원래의 행렬과 모든 요소가 일치합니다. I를 왼쪽에서 곱해도 같은 결과가 나옵니다.
※ 주석 1
문헌에 따라서는 단위 행렬이 아닌, 모든 성분이 1인 행렬을 unit matrix라고 부르기도 합니다.
[딥러닝 입문 - 4] 선형 대수의 기초(5/9)
4.1.8. 역행렬 0이 아닌 스칼라 x의 역수로 x의 -1승을 생각할 수 있습니다. 행렬 역수에 대응하는 것이 역행렬(inverse matrix)입니다. 정확한 정의는 다음과 같습니다. 행렬 A에 대하여, AB=I, BA=I 를 충
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 4] 선형 대수의 기초(8/9) (0) | 2020.07.26 |
|---|---|
| [딥러닝 입문 - 4] 선형 대수의 기초(7/9) (0) | 2020.07.24 |
| [딥러닝 입문 - 4] 선형 대수의 기초(6/9) (0) | 2020.07.22 |
| [딥러닝 입문 - 4] 선형 대수의 기초(5/9) (0) | 2020.07.19 |
| [딥러닝 입문 - 4] 선형 대수의 기초(3/9) (0) | 2020.07.17 |
| [딥러닝 입문 - 4] 선형 대수의 기초(2/9) (0) | 2020.07.16 |
| [딥러닝 입문 - 4] 선형 대수의 기초(1/9) (0) | 2020.07.15 |
| [딥러닝 입문 - 3] 미분의 기초 (3/3) (0) | 2020.07.12 |



