4.1.8. 역행렬
0이 아닌 스칼라 x의 역수로 x의 -1승을 생각할 수 있습니다. 행렬 역수에 대응하는 것이 역행렬(inverse matrix)입니다.
정확한 정의는 다음과 같습니다. 행렬 A에 대하여, AB=I, BA=I 를 충족시키는 행렬 B를 A의 역행렬이라고 합니다. 이러한 조건을 만족하는 행렬 B는 행렬 A에 의해 존재하거나 존재하지 않을 수 있습니다. 그러나 만약 A에 대하여 이 조건을 만족하는 행렬이 존재한다면, 그러한 행렬은 단지 하나뿐으로 알려져 있습니다. 그래서 행렬 A의 역행렬은 A의 -1승으로 표기합니다.
역행렬의 정의에서

가 성립한다는 점에 유의하십시오. 여기에서 I 는 단위행렬입니다.
역행렬이 존재하는 행렬을 가역 행렬이라고 합니다. 가역 행렬이 되려면 적어도 행렬 곱

와
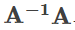
가
양쪽 다 정의되어 있지 않으면 안 됩니다. 이것은 A는 정칙 행렬(즉, 행과 열 개수가 같은 행렬) 임을 의미합니다(왜인지 생각해보십시오). 그러나, A의 행수와 열수가 같다고 항상 A가 정칙 행렬인 것은 아닙니다. 정칙 행렬의 조건에 대한 자세한 설명은 여기서는 생략합니다.
크기가 2 × 2 나 3 × 3 같은 작은 행렬의 경우에는 손으로도 계산 가능한 역행렬 계산법이 알려져 있지만, 기계 학습은 더 큰 행렬(1000 × 1000 등)을 처리할 수 있고, 그런 큰 행렬의 역행렬을 컴퓨터를 사용하여 효율적으로 계산하는 방법이 연구되고 있습니다.
4.1.9. 선형 결합과 이차 형식
기계 학습의 수식에서 자주 나오는 형식 중에
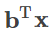
와
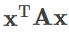
의 두 가지가 있습니다. 전자는 선형 결합 또는 일차 결합, 후자는 이차 형식이라고 합니다. 스칼라의 일차식과 이식을 벡터로 확장한 것으로 파악하시면 좋습니다.
선형 결합의 계산을 요소별로 살펴보면,
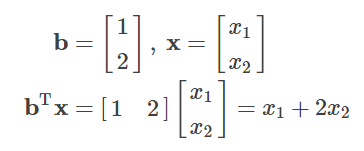
처럼, x의 요소인 x1 및 x2에 관하여 일차식으로 되어 있습니다.
또한, 이차 형식도 마찬가지로 요소마다 확인해 보면,

가 되고, 각 요소에 대해 이차 식으로 되어 있습니다. 일반적으로 x1,…, xN에 관한 이차 함수는

로,

로
표기할 수 있습니다. 여기에서 A는 2차 항의 계수를 나타내는 크기 (n, n)의 행렬, b는 1차 항의 계수를 나타내는 n 차원의 벡터, c는 스칼라의 정수 부분입니다.
[딥러닝 입문 - 4] 선형 대수의 기초(6/9)
4.1.10. 벡터에 의한 미분과 기울기 미분은 입력값이 변화할 경우의 함숫값의 변화량에서 구했습니다. 이것은 함수의 입력 벡터인 경우에도 마찬가지입니다. 벡터를 입력받는 함수의 미분을 생
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 4] 선형 대수의 기초(9/9) (0) | 2020.07.28 |
|---|---|
| [딥러닝 입문 - 4] 선형 대수의 기초(8/9) (0) | 2020.07.26 |
| [딥러닝 입문 - 4] 선형 대수의 기초(7/9) (0) | 2020.07.24 |
| [딥러닝 입문 - 4] 선형 대수의 기초(6/9) (0) | 2020.07.22 |
| [딥러닝 입문 - 4] 선형 대수의 기초(4/9) (0) | 2020.07.18 |
| [딥러닝 입문 - 4] 선형 대수의 기초(3/9) (0) | 2020.07.17 |
| [딥러닝 입문 - 4] 선형 대수의 기초(2/9) (0) | 2020.07.16 |
| [딥러닝 입문 - 4] 선형 대수의 기초(1/9) (0) | 2020.07.15 |



