
3.5 선형성
미분은 선형성이라는 성질을 가지고 있습니다. 구체적인 예를 들어 살펴봅시다.
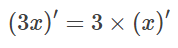
처럼 상수를 미분 연산의 외측으로 꺼낼 수 있습니다. 또한,

처럼, 덧셈과 뺄셈은 각 항목마다 독립적으로 미분 연산을 할 수 있습니다. 이 두 가지 특성을 합쳐 '선형성'이라고 합니다.
좀 더 미분 계산을 해봅시다.
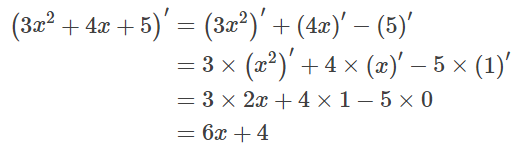
이 선형성에 관해서는 아래와 같은 공식으로 요약할 수 있습니다.

두 함수의 곱의 형태로 작성된 함수에 관해서는 다음의 공식이 성립됩니다.
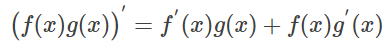
함수 f의 도함수와 함수 g의 도함수를 알면, 함수 fg를 계산할 수 있다는 것을 알 수 있습니다.
3.6. 합성 함수의 미분
함수 y=f(x) 와 z=g(y)의 합성과 f를 적용한 후에 g을 적용하는 함수, 즉 z=g(f(x))의 수를 말합니다. 딥러닝에 이용되는 신경망은 여러 층으로 겹쳐서 복잡한 함수를 표현합니다. 각 층을 하나의 함수로 간주하면 신경망은 많은 함수(층)를 합성한 합성 함수라고 볼 수 있습니다. 합성 함수의 미분에는 다음에 소개하는 공식(합성 함수의 미분 공식)이 유용합니다. 이 공식은 연쇄 법칙(chain rule)이라고도 합니다. 연쇄 법칙은 합성 함수 미분을 쉽게 계산하는 공식일 뿐만 아니라 신경망 훈련 방법인 오차 역전파법을 이해하는 데 필수적인 역할을 합니다.
간단한 예로,

를 계산하는 것을 봅시다. 이 수식은 3x+4라는 안쪽 부분과 제곱의 바깥 부분으로 구성되어 있습니다.
이 식을

와 같이 전개하여 미분을 계산해도 좋지만, 3승이나 4승으로 증가하면 식을 전개하는 것이 힘들어집니다. 여기서 유용한 개념이 합성 함수의 미분입니다. 합성 함수의 미분은 내부의 미분과 외부의 미분을 각각 실시하고, 그 결과를 곱함으로써 구할 수 있습니다. 외부의 미분 시에는 함수의 인수를 입력으로 간주하고, 그 입력에 대한 미분을 계산합니다.
그럼 구체적으로 이 (3x+4)의 제곱 함수의 미분을 해보겠습니다. 먼저 내부의 함수를 u=(3x+4)로 두면,

가 됩니다. 여기에서(⋅)′를 좀 더 엄밀하게 생각할 필요가 있습니다. 지금 변수는 x, u의 두 개가 있기 때문에, (⋅)′라는 표기는 x에서 미분하고 있는지 u에서 미분하고 있는지 구별이 안됩니다. 그래서 다소 복잡하게 보이지만, 조금 전에 소개한 d를 사용한 기법을 이용하여 미분 변수를 명시합니다.
합성 함수의 미분을 공식으로 정리하면 다음과 같습니다.
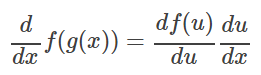
여기에서 u=g(x)입니다.
공식을 보는 것보다 실제 적용하는 것이 이해하기 쉬울지도 모릅니다. 합성 함수의 미분 공식을 이용하여 좀 전의(3x+4)의 제곱의 미분을 계산하면 다음과 같이 됩니다. 두 번째 줄에서 합성 함수의 미분 공식을 이용하고 있는 것에 주목하십시오.

관심 있으신 분은 (3x+4)의 제곱을 전개하여 각 항을 미분한 경우와 계산 결과가 일치하는지 확인해 보세요.
3.7. 편미분
기계 학습은 하나의 입력 변수 x에서 출력 변수 y를 예측하는 경우는 드물며, 많은 경우 여러 입력 변수 x1,x2,…,xM 를 이용하여 y를 예측하는 다변수 함수가 사용됩니다. 예를 들어, 임대료를 예측하는 경우, 방의 넓이뿐만 아니라, 역에서의 거리와 주변의 생활환경도 동시에 고려하는 것이 더 정확하게 예측할 수 있을 것으로 기대됩니다. 여러 입력 x1,x2,…,xM 을 취하는 함수 f(x1,x2,…,xM)를 다변수 함수라 부릅니다. 이 다변수 함수에서의 입력 xM에만 주목하고 미분하는 것을 편미분이라 부르며,

로 표현합니다. 미분을 의미하는 기호가 d에서 ∂로 변했습니다. 이렇게 하면 ∂xm은 xm 이외를 상수로 간주, xm에만 착안하여 미분을 한다는 의미입니다(※주석 3).
(※주석 3)
입력 변수가 다른 입력 변수와 독립되지 않는 경우는 상수로 간주할 수 없습니다. 그러나 본 문서에서는 이러한 경우는 나오지 않습니다.
다음 예에서 구체적인 계산의 흐름을 확인해 봅시다.

편미분에서도 미분과 같은 공식을 적용할 수 있습니다. 이번 경우에는 x1에만 주목하고 있으며, x2는 상수로 사용되고 있습니다. 따라서 위 식의 두 번째 줄에서 세 번째 줄 x2를 x1으로 편미분한 값을 0으로 하고 있습니다(상수의 미분은 0 임을 기억하세요).
[딥러닝 입문 - 4] 선형 대수의 기초(1/9)
4. 선형 대수의 기초 기계 학습의 이론에는 선형 대수학에서 사용되는 개념이 많이 등장합니다. 이러한 개념을 이용함으로써 복수의 값이나 변수를 한꺼번에 처리할 수 있도록 수식을 간결
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 4] 선형 대수의 기초(4/9) (0) | 2020.07.18 |
|---|---|
| [딥러닝 입문 - 4] 선형 대수의 기초(3/9) (0) | 2020.07.17 |
| [딥러닝 입문 - 4] 선형 대수의 기초(2/9) (0) | 2020.07.16 |
| [딥러닝 입문 - 4] 선형 대수의 기초(1/9) (0) | 2020.07.15 |
| [딥러닝 입문 - 3] 미분의 기초 (2/3) (0) | 2020.07.11 |
| [딥러닝 입문 - 3] 미분의 기초 (1/3) (1) | 2020.07.10 |
| [딥러닝 입문 - 2] 머신 러닝에 사용되는 수학 (5) | 2020.07.07 |
| [딥러닝 입문 - 1] 딥러닝 시작하기 (0) | 2020.07.04 |



