4.1.4 행렬 곱
행렬의 곱셈은 행렬 곱, 외적 ,요소적(아다마르 곱)등 여러 가지가 있습니다. 여기서는 그중에서 선형 대수와 기계 학습에 자주 등장하는 행렬 곱에 대해 설명합니다.
행렬 A와 행렬 B의 행렬 곱은 AB로 쓰고, A의 각 행과 B의 각 열의 내적을 나열한 것으로 정의됩니다. 예를 들어, 행렬 A의 1행의 행 벡터와, 행렬 B의 1열의 벡터의 내적 결과는 A와 B 행렬 곱의 결과를 나타내는 행렬 C의 1행 1열에 대응합니다.
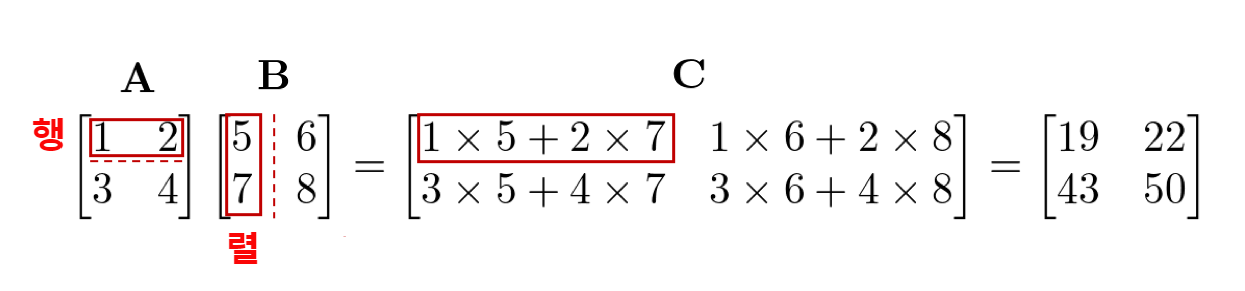
내적이 정의되는 조건으로 벡터의 크기가 같지 않으면 안 됩니다. 이 조건은 성립되어야만 합니다.
구체적으로는,

일 때, AB = C 행렬 곱을 정의하기 위해서는, A의 열수 M과 B의 행수 O가 일치해야 합니다(※주석 1). 즉,
M = O가 아니면 안 됩니다. 그리고 결과 행렬 C의 행과 열 수는 A의 행 수 N과 B의 열 수 P와 각과 같습니다.
즉
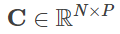
입니다.
두 N차원 벡터 x, y의 내적은 x를 사이즈 (1,N)의 행렬(즉 행 벡터), y를 사이즈 (N,1)의 행렬(즉 열 벡터)로 간주하여 행렬 곱을 할 것으로 생각할 수 있습니다. 두 벡터의 행렬 곱은 사이즈가 (1,1)인 행렬, 즉 스칼라입니다. 이것은 두 벡터의 내적의 결과가 스칼라가 되는 것과 일치합니다.

행렬 곱은 AB와 BA가 동일하다고 할 수 없다는 점에서 스칼라 곱과 크게 다릅니다. 예를 들어,

라면,
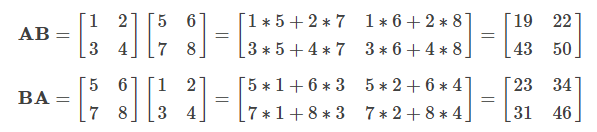
가 되고, AB ≠ BA 입니다. 곱셈의 순서의 차이를 명시적으로 표현하는 경우 행렬 A에 행렬 B를 왼쪽부터 곱하는 것(BA의 계산)을 행렬 B를 매트릭스 A에 좌승(左乗)한다고 하며, 오른쪽에서 곱하는 경우는 우승(右乗)한다고 합니다.
A와 B의 선택에 따라 AB와 BA가 동일한 경우도 있습니다. 예를 들어,

라면,

가 되어, AB와 BA는 일치합니다. 그러나 여기서 주의할 점은 「어떤 A,B 라도 AB = BA 가 성립한다」는 주장은 잘못되었다는 것입니다.
그러면, 행렬의 계산 조건도 확인하면서, 다음 3가지 연습 문제의 계산을 한번 해 보십시오.
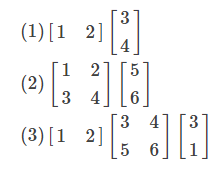
정답은 아래와 같습니다.

이러한 계산은 기계 학습의 기초를 학습해가는 과정에서 자주 등장합니다. '행렬 곱'에서는 연산 전후의 행 · 열 수의 변화에 꼭 주의하시기 바랍니다.
※주석 1
N × M행렬일 때, N과 M중에서 어느 게 행이고 어느 게 열일까? 잘 모르겠는 경우에는 '매트릭스'라는 말을 다시 떠올리며 "행 → 열"로, 즉 먼저 오는 N이 행이고, M이 열 이라고 생각하는 것을 추천합니다.
[딥러닝 입문 - 4] 선형 대수의 기초(4/9)
4.1.5. 행렬 곱에 의한 벡터 행렬의 크기 변화 행렬의 전후에서는 행렬의 형태가 변화합니다. 구체적으로는 크기가 (L, M)과 (M, N)인 행렬의 행렬 곱 결과는 크기가 (L, N)인 행렬이 됩니다. 앞의 3개
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 4] 선형 대수의 기초(7/9) (0) | 2020.07.24 |
|---|---|
| [딥러닝 입문 - 4] 선형 대수의 기초(6/9) (0) | 2020.07.22 |
| [딥러닝 입문 - 4] 선형 대수의 기초(5/9) (0) | 2020.07.19 |
| [딥러닝 입문 - 4] 선형 대수의 기초(4/9) (0) | 2020.07.18 |
| [딥러닝 입문 - 4] 선형 대수의 기초(2/9) (0) | 2020.07.16 |
| [딥러닝 입문 - 4] 선형 대수의 기초(1/9) (0) | 2020.07.15 |
| [딥러닝 입문 - 3] 미분의 기초 (3/3) (0) | 2020.07.12 |
| [딥러닝 입문 - 3] 미분의 기초 (2/3) (0) | 2020.07.11 |



