4.5.1 계산 예 1
합성 함수의 미분을 사용하여 다변수 함수의 미분을 구체적으로 계산해 봅시다.

로

합니다.
즉, g는 2 입력 4 출력, f는 4 입력 3 출력입니다.
이들에 대하여
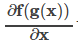
를 계산합니다.
편미분을 정의대로 계산하면

가 됩니다(행렬 중,

등은 본래는

로 작성해야 하지만, 수식이 복잡해지기 때문에 생략했습니다).
따라서, 합성 함수의 미분 공식으로부터

가 됩니다. 공식을 적용할 때 u = g(x) 즉

를 사용했습니다.
4.5.2 계산 예 2
또 다른 예로, 합성 함수의 입출력이 1 변수가 될 때, 즉 M=1, L=1의 경우를 생각해 봅시다. 식을 단순화하기 위해, N=2로 합니다. 1 변수 임을 강조하고, u=g(x), y=f(u)와 스칼라 변수는 소문자를 사용합니다. f와 g를 합성한 함수를 h(x)=f(g(x)) 로 합니다. h는 입출력이 모두 1 변수이므로 그 미분을 간편하게 h′(x)라고 하면 합성 함수의 미분 공식은

로 적어 내려갈 수 있습니다(미분하는 변수가 1개밖에 없는 경우는 편미분 기호 ∂ 대신 1 변수 미분 d를 사용했습니다).
본 자료에서 소개한 합성 함수의 미분 공식 외에도 행렬과 벡터의 계산에 사용되는 공식은 많습니다. 그 공식은 The Matrix Cookbook 등으로 정리되어 있기 때문에, 논문 등을 읽을 때에도 필요에 따라 참조하면 좋을 것입니다. 또한 야코비 행렬의 계산 방법은 The Matrix Calculus You Need For Deep Learning에 정리되어 있습니다.
The Matrix Calculus You Need For Deep Learning
This paper is an attempt to explain all the matrix calculus you need in order to understand the training of deep neural networks. We assume no math knowledge beyond what you learned in calculus 1, and provide links to help you refresh the necessary math wh
arxiv.org
[딥러닝 입문 5] 확률·통계의 기초(1/5)
5. 확률 · 통계의 기초 여기서는 기계학습에 이용하는 확률, 통계의 개념과 용어를 설명합니다. 세상에는 '무작위'로 일어나는 사건이나 배경의 메커니즘을 모르기 때문에 무작위로 취급해야만
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 5] 확률·통계의 기초(4/5) (0) | 2021.03.09 |
|---|---|
| [딥러닝 입문 5] 확률·통계의 기초(3/5) (0) | 2021.02.22 |
| [딥러닝 입문 5] 확률·통계의 기초(2/5) (0) | 2021.02.12 |
| [딥러닝 입문 5] 확률·통계의 기초(1/5) (0) | 2021.01.18 |
| [딥러닝 입문 - 4] 선형 대수의 기초(8/9) (0) | 2020.07.26 |
| [딥러닝 입문 - 4] 선형 대수의 기초(7/9) (0) | 2020.07.24 |
| [딥러닝 입문 - 4] 선형 대수의 기초(6/9) (0) | 2020.07.22 |
| [딥러닝 입문 - 4] 선형 대수의 기초(5/9) (0) | 2020.07.19 |



