
5.4 조건부 확률
앞에서는 복수의 확률 변수를 동시에 고려하는 방법으로서 동시 확률 및 동시 분포 개념, 동시 확률과 하나하나의 확률 변수에 주목했을 때의 확률(주변 확률) 사이의 관계를 주변화라는 계산방법으로 설명했습니다. 이번에는 "어떤 사건(사상)이 일어난 조건하에서 다른 사건이 일어날 확률"을 의미하는 조건부 확률(conditional probability)이라는 개념을 설명합니다. 앞에서 다루었던 확률은 우선 대상으로 하는 현상에 대해 고려할 수 있는 모든 사건을 따져, 그중 대상으로 하는 사건이 일어날 확률은 얼마인가 였습니다. 한편, 조건부 확률은 생각할 수 있는 사건 중 특정 조건을 만족하는 사건을 먼저 정하고, 거기에 이어서 원하는 사건이 일어날 확률을 구하는 것입니다.
예를 들어, 가게에 온 사람(이하 손님)이 우산을 가지고 있을 때를 1, 없을 때를 0으로 취하는 확률 변수가 X라고 합시다. 또한, 어떤 손님이 왔을 때, 밖에 비가 오고 있으면 1, 비가 오지 않으면 0을 취하는 확률 변수를 Y라고 합시다. '손님이 우산을 가지고 있었는지'와 '그 순간에 비가 내리고 있었는지 여부'라는 두 가지 정보가 쌍으로 된 데이터가 16개 있다고 합시다. 16명의 손님을 관찰하고 데이터를 모으면 아래와 같습니다.
|
우산(X) |
비(Y) |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
0 |
1 |
|
0 |
1 |
|
0 |
1 |
|
1 |
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
0 |
이러한 데이터에서 확률 변수 X, Y의 동시 분포표를 작성하면 다음과 같습니다.
|
|
Y = 0 |
Y = 1 |
|
X = 0 |
6 / 16 |
3 / 16 |
|
X = 1 |
1 / 16 |
6 / 16 |
그럼 "손님이 우산을 갖고 있었다(X=1)"라는 조건하에서 "그때 비가 오지 않았다(Y=0)"라는 확률은 얼마나 될까요?
우선, "손님이 우산을 갖고 있었다(X=1)"라는 상황의 데이터만 위의 결합 분포표에서 가져옵시다.
|
우산(X) |
비(Y) |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
0 |
총 7개의 데이터가 있고, 이 중 "비가 오지 않았다(Y=0)"인 데이터는 1개입니다. 즉, "고객이 우산을 가지고 있다는 조건 하에서 그때 비가 오지 않았다"의 확률은 1/7입니다. 이는 다음과 같이 표기할 수 있습니다.

이것이 조건부 확률이라 불리는 것으로, 조건이 되는 사건을 막대 | 다음에 쓰고, 그 조건하에서의 다음 사건을 막대 | 앞에 씁니다. 마찬가지로, "손님이 우산을 가지고 있는 조건하에서 마침 비가 내리고 있을 확률"은 위 표에서 6/7입니다.
따라서, 다음이 성립합니다.

이러한 두 가지 확률이 각각
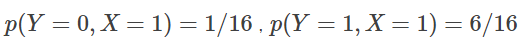
와 같은 동시 확률과는 다르다는 것을, 위의 동시 분포표와 비교하면서 확인해 봅시다.
"손님이 우산을 갖고 있고 밖에는 비가 내린다"의 동시 확률은 6/16 입니다만, "손님이 우산을 가지고 있다는 조건하에서 밖에 비가 내린다"는 조건부 확률은 6/7입니다.
동시 확률은
「손님이 우산을 갖고 있지 않고 밖에 비가 온다」
「손님이 우산을 갖고 있지 않고 밖에 비가 오지 않았다」
「손님이 우산을 갖고 있고 밖에 비가 오지 않았다」를 포함한 모든 사건을 고려해 그 안에서 대상으로 하는 사건
「손님이 우산을 갖고 있고 밖에 비가 온다」이 일어날 확률을 의미합니다.
한편, 조건부 확률은 지금 조건이 되는 사건(사상)인 「손님이 우산을 갖고 있다」라는 사건(사상)만을 우선 대상으로 하고, 그중에서도 주목하고 있는 사건(사상) 「밖에 비가 내린다」가 일어날 확률을 구합니다. 각각의 확률 값을 계산할 때 분모가 다르다는 것을 주목하십시오.
또한 위의 두 조건부 확률을 더하면 1이 됩니다. "어떤 조건 하에서"라는 제약에서 대상으로 하는 확률 변수가 취할 수 있는 값의 모든 확률을 나란히 나열하는 것을 조건부 분포(conditional distribution)라고 하며, 그 확률을 모두 더하면 반드시 1이 됩니다. 위의 예는 다음 계산으로 확인할 수 있습니다.

여기서 확률 변수 X가 취할 수 있는 실제 값 중 하나를 나타내는 문자를 x로,
확률 변수 Y가 취할 수 있는 실제 값 중 하나를 나타내는 문자를 y로 사용하면
일반적으로 조건부 확률은 다음과 같이 정의됩니다.

이때, 조건부 분포를 충족하는 조건은 다음과 같이 나타낼 수 있습니다.

여기에서

는 반드시 1이 되지 않는다는 점에 유의하십시오.
그럼, 위의 조건부 확률의 정의를 이용하여 동시 확률과 주변 확률로부터 조건부 확률을 다시 계산하여 봅시다.

물론, 위에서 다른 방법으로 구한 조건부 확률과 일치합니다.
그런데 위에서 언급한 동시 확률과 조건부 확률의 관계에 대해 다시 생각해 봅시다. 위의 「조건부 확률의 정의」의 식을 변형하면 다음과 같이 됩니다. 앞으로는 간단하게, 확률 변수의 설명을 생략하고, p(X=x)를 p(x)로 표기합니다. 확률 변수 X에 의해 x라는 값으로 매핑 가능한 사건이 발생할 확률을 뜻합니다. 마찬가지로, p(Y=y)를 p(y)로 표기합니다.

동시 확률은 조건부 확률에 그 조건이 되는 사건(사상)이 발생할 확률(주변 확률)을 곱하여 얻을 수 있다는 것을 알 수 있습니다.
이번 예제에서는 "비가 오는지 여부"에 의해 "손님이 우산을 갖고 있는가"가 영향을 받기 때문에 두 확률 변수 Y, X는 종속 (dependent)입니다. 한편, 예를 들어 「손님이 왔을 때, 비가 내리고 있었는가」와 「내가 지금 배가 고픈지」가 전혀 무관하다고 합시다. 후자의 배가 고프다는 사건을 1로, 배가 고프지 않다는 사건을 0으로 매핑하는 확률 변수 Z를 도입하면, Y와 Z는 지금 독립(independent)인 상황입니다.
이때, Z의 실현 값을 z로 하고, 조건부 확률 p(y|z)는 Y가 어떻게 될지, Z와 전혀 관계없기 때문에 p(y)와 동일합니다. 조건을 줘도, 주지 않아도 결과가 변하지 않기 때문입니다. 이를 이용하면, y와 z의 동시 확률은 다음과 같이 변형할 수 있습니다.

Y와 Z가 독립적이기 때문에, p(y|z)=p(y)가 되는 것을 사용했습니다.
이 식에서 두 확률 변수가 독립적일 때, 동시 확률은 각각의 주변 확률의 곱으로 쓸 수 있다고 하겠습니다.
5.5 베이즈의 정리
앞에서 설명한 조건부 확률은, 어떤 전제가 성립되는 상황에서 주목하는 사건(사상)이 발생할 확률을 설명하기 위한 것이었습니다. 이것은 「어떤」 원인이 생겼다는 조건하에서 어떤 「결과」가 발생할 확률을 구하고 파악할 수 있습니다. 그럼, 역으로 「어떤」 결과가 관측되었을 때 어떤 현상이 '원인'일 확률은 어떻게 구하면 좋을까요? 지금 일어날 수 있는 사건을 확률 변수 X로 표시하고, 결과가 될 수 있는 사건을 확률 변수 Y로 표현합니다. 이때, 원인으로서 x의 관측을 토대로 결과가 y가 될 확률을 조건부 확률
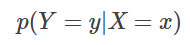
로 표시했습니다.
앞의 정의에서, 여기에 원인 x가 원래 발생할 확률 p(X=x)를 곱하면 동시 확률 p(Y=y, X=x)가 됩니다. 즉

입니다. 그럼, 결과가 y였다는 관측 하에서 원인이 x일 확률은 어떻게 표현할까요? 이것은 위의 '조건 사건'과 '주목 사건'을 바꾼 조건부 확률로

라고 쓸 수 있습니다. y라는 결과 관측을 토대로 그 근원이 x일 확률을 의미합니다. 여기에 결과 y가 원래 발생할 확률 p(Y=y)를 곱하여 조합해보면, 조건부 확률의 정의로부터

도출됩니다. 여기서, 식(1)과 식(2)의 우변이 같다는 것에 주목합시다.
그러면 식(1)과 식(2)의 좌변끼리도 등호로 연결이 가능하며,

이 성립되는 것을 알 수 있습니다.
이 식을 변형하여, 구하려는 「결과가 y가 되었다는 조건 하에서 원인이 x일 확률」을 좌변에 두면

가 도출됩니다. 이것을 베이즈 정리(Bayes 'theorem)라고 합니다.
따라서 어떤 결과가 관측되었을 때, 어떤 사건(사상)이 원인일 가능성은
-
원인으로 생각하는 사건이 (결과와 관계없이) 원래 발생할 확률 ( p(X=x) )
-
결과로 관측한 사건이 (원인에 관계없이) 원래 발생할 확률 ( p(Y=y) )
-
고려하는 원인이 실제 했다는 조건하에서 관측된 결과가 발생할 확률 ( p(Y=y|X=x) )
의 세 가지로부터 구할 수 있습니다. 베이즈 정리에 등장하는 좌변의 조건부 확률과 우변의 분자에 있는 주변 확률은 특별한 호칭이 있습니다.
먼저 우변의 분자에 있는 주변 확률(위 식에서는 p(X=x))은 「결과」가 관측하기 전에 (사전)에 원인 x가 애초에 발생할 확률을 나타내므로, 사전 확률(prior probability)이라고 합니다.
한편, 왼쪽의 조건부 확률(위 식에서는 p(X=x|Y=y))은 어떤 「결과 y」가 관측되었다는 조건 하에서 (사후에) 원인 x가 발생한 확률을 나타내므로 사후 확률(posterior probability)이라고 합니다.
베이즈 정리의 응용 사례로 스팸메일 필터가 있습니다.
우선, N개의 주목하는 단어

를 정합니다( "sale", "buy", "free"... 등).
그리고 메일에 어떤 단어 wi가 포함된 경우 1이 되고, 포함되지 않는 경우 0이 될 확률 변수를 Wi로 하여, "메일에 어떤 단어 wi가 포함될 확률"을 아래와 같이 나타냅니다.
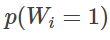
다음으로, 메일이 스팸인 경우 1이 되고, 스팸이 아닌 경우 0이 될 확률 변수를 Y로 하여 "스팸 메일의 존재 확률"을 p(Y=1)로 표기합니다. 이때 「어느 메일이 스팸이었다는 상황에서 단어 wi가 포함되어 있었다」라는 확률은

가 됩니다. 그러면, 예를 들어 wi와 wj가 모두 포함된 경우 동시 확률
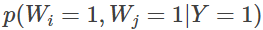
를 고려하게 되겠지만 각 단어가 독립적으로 나타난다고 가정하면, 이것은

로 분해할 수 있습니다. 여기에 세상의 많은 메일들을 대량으로 모으고, 각 단어가 어떤 확률로 나타나는지 살펴보면
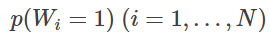
가 구해집니다. 또한 수집한 이메일에서 스팸 메일만 추출합니다. 그러면 메일이 스팸일 확률 p(Y=1)이 구해집니다. 또한 그 스팸 메일에 포함된 단어를 검사하여 단어가 어떤 확률로 출현하고 있는지를, 주목하고 있는 모든 단어에 대해 구하면,
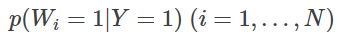
이 모두 구해집니다. 이들을 이용하면, "어떤 메일에 단어 wi, wj, wk,… 가 포함되어 있을 때, 그 메일이 스팸일 가능성"을 다음과 같이 계산할 수 있습니다.

[딥러닝 입문 5] 확률·통계의 기초(3/5)
5.6. 우도(尤度)와 최우추정법 앞에서 「확률 변수가 취할 수 있는 다양한 값에 확률을 대응시키는」 확률 분포를 표 형태로 표현했습니다. 여기서 확률 변수 X가 x값을 취할 확률 p(X=x)를, 표 대신
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(1/4) (0) | 2021.05.30 |
|---|---|
| [딥러닝 입문 5] 확률·통계의 기초(5/5) (0) | 2021.05.15 |
| [딥러닝 입문 5] 확률·통계의 기초(4/5) (0) | 2021.03.09 |
| [딥러닝 입문 5] 확률·통계의 기초(3/5) (0) | 2021.02.22 |
| [딥러닝 입문 5] 확률·통계의 기초(1/5) (0) | 2021.01.18 |
| [딥러닝 입문 - 4] 선형 대수의 기초(9/9) (0) | 2020.07.28 |
| [딥러닝 입문 - 4] 선형 대수의 기초(8/9) (0) | 2020.07.26 |
| [딥러닝 입문 - 4] 선형 대수의 기초(7/9) (0) | 2020.07.24 |



