
5.7. 사후 확률 극대화 추정 (MAP 추정)
앞에서 해설한 최우추정은 많은 경우에 유용하지만, 요청 매개 변수에 대해 어떤 사전 지식이 있어도 그것을 활용할 수 없습니다. 따라서 샘플 크기가 작은 경우에, 말도 안 되는 결과가 나올 수 있습니다. 구체적인 예를 살펴봅시다.
다시 동전의 앞/뒷면이 나올 확률을 추정하는 예를 살펴봅시다. 동전을 5번 던진 결과, 우연히 5번 모두 앞면이 나왔다고 합시다. 이 경우, 앞에서 설명한 것과 동일한 확률 모델을 이용해 우도를 계산하고 최우추정으로 모델 매개변수를 결정하면

를 충족하면서 이번 관측 데이터상에서 우도
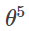
를 최대로 하는 θ는 1입니다.
이것은 "앞면이 나올 확률이 1, 뒷면이 나올 확률은 0" 이라는 추정 결과를 얻게 된 것을 의미합니다. 만약 '뒷면이 나올 확률도 0보다 클 것이다'라는 사전 지식을 가지고 있으며 그것을 활용할 수 있다면, 이번 같은 경우에도 보다 나은 추정을 할 수 있을 것입니다.
사전 지식도 고려하면서 관측 데이터를 바탕으로 확률 모델의 매개 변수를 추정하는 방법에는 사후확률극대화(maximum a posteriori 이후 MAP) 추정이 있습니다. MAP추정은, 대상 데이터의 확률 분포를 나타내는 확률 모델의 파라미터를 데이터를 이용하여 결정하지만 데이터뿐만 아니라 매개 변수도 확률변수라고 생각하는 점이 최우추정법과는 다릅니다.
매개 변수를 확률변수

라고 하면
이 매개 변수가 어떤 값을 취할지를 나타내는 분포
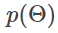
를 도입할 수 있습니다.
이것을 사전 분포(prior distribution)라고 부르며, 여기에 "구하고자 하는 매개 변수에 대한 사전 지식"을 반영할 수 있습니다. 여기에서

가 될 확률인

(이후 p(θ)로 표기)를 데이터의 확률 모델
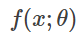
과는 별개의 확률 모델
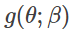
로 나타내면, β를 인위적으로 주거나,
이러저러한 방법으로 결정해 두는 것으로 '어떤 θ가 일어나기 쉽다'라는 사전 지식을 표현할 수 있습니다.
MAP 추정은 관측 데이터

가 관측되었다는 조건 하에서 가장 확률이 커지는 θ를 구합니다. 즉,
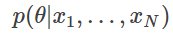
를 최대로 하는 θ를 구합니다. 이것은

가 관측되었다는 결과를 두고,
"데이터의 확률 분포를 나타내는 모델의 매개 변수가 θ였음이 원인"이라는 확률을 의미하기 때문에 사후 확률이라고 합니다.
베이즈 정리에서 사후 확률은

로 표기했었습니다. 오른쪽에 주목해 주세요. 분자의

를 확률 모델 f(x;θ)를 이용하여

로 나타내면, 이것은 관측 데이터

하에서의 확률 모델 f(x;θ)의 우도입니다.
또한 그 오른쪽 p(θ)는, 매개 변수가 θ이라는 값이 되는 사전 확률이었습니다. 이것이
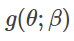
라는 확률 모델로 표현된다고 합시다.
지금 사후 확률을 최대화하는 파라미터 θ를 구하기 위해, 우변을 최대화하는 θ를 생각해봅시다.
이때, 매개 변수와 무관하게 결정되는 분자

는 무시하고, 분모

에만 주목하여
이를 최대화하는 매개 변수 θ를 결정하면, 그 θ는 구하고 싶은 좌변의 사후 확률을 최대화하는 θ와 일치합니다. 위 식은, 우도와 사전 분포의 곱으로 되어있습니다. 이로부터 사후 분포는 우도와 사전 분포의 곱에 비례한다는 것을 알 수 있습니다.
5.7.1. 예 : 동전 던지기에서의 매개변수 추정
앞의 최우추정을 이용한 동전 던지기의 예를 다시 생각해봅시다. 이번에는 MAP 추정을 사용하여 매개변수를 추정하여 봅시다. 사용할 데이터는 아까와 동일한 10회 동전 던지기 결과입니다. 또한 확률 모델 f(x;θ)도 동일하게 최우추정과 동일한 것을 사용합니다. MAP 추정은 확률 모델 f(x;θ) 이외에도 사전 분포 p(θ)를 설계할 필요가 있습니다. p(θ)의 결정 방법은 추정할 사람이 어떤 사전 지식(또는 신념)을 가지고 있느냐에 따라 자유롭게 선택할 수 있지만, 여기서는 사전 분포를
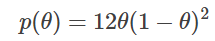
로 설정합니다.
그래프로 그리면 p(θ)는

에서 최댓값을 갖는다는 것을 알 수 있습니다.
이것은, 「동전 던지기가 행해지기 전에는, 실험자에게는 θ=1/3 가 가장 있을 수 있는 가능성입니다.」
즉, "이 동전은 앞보다 뒷면이 더 나오기 쉽다"라고 믿고 있다(사전 지식을 갖고 있다)고 해석할 수 있습니다.
사후 분포는 θ의 함수로서
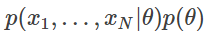
에 비례하는 것이었습니다.
이를 구체적으로 계산하면

가 됩니다. 이것을 θ의 함수로서 최대화합니다. 최우추정의 경우와 마찬가지로,
이 값 자체가 아닌 대수를 취한 값을 최대화하는 θ를 구합니다.
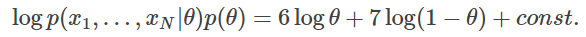
여기에서 const. 는 θ에 의존하지 않는 상수(구체적으로는 log12)로, 값을 최대로 하는 θ를 결정하는데 영향을 주지 않습니다.
이를 θ로 미분한 것이 0과 동일하다는 방정식을 세우면,

로 풀 수가 있습니다. 이것이 MAP 추정에서 얻은 추정치입니다.
최우추정에서 얻어진 추정치는 θ=1/2 이었기 때문에 MAP 추정은 최우추정보다 낮게 θ를 추정하고 있다는 것을 알 수 있습니다. 이것은 사전 분포 p(θ)에 의해 θ는 1/2보다 작은 값이 나타나기 쉽다는 사전 지식을 반영하고 있습니다. 반대로 사전 분포에 큰 θ가 나타나기 쉽다는 사전 지식을 넣으면 MAP 추정값을 최우추정법보다 크게 할 수 있습니다.
이 예에서도 알 수 있듯이, MAP 추정은 사전 분포의 설정에 의해 얻어지는 추정치가 변화합니다. 이 것은 MAP 추정법이 사전 지식으로 유연한 모델링이 가능한 반면 잘못된 사전 지식을 바탕으로 사전 분포를 설계하면 추정치와 실제 데이터 사이의 괴리가 발생할 가능성이 있다는 것을 의미합니다.
[딥러닝 입문 5] 확률·통계의 기초(5/5)
5.8 통계 여기서는 몇 가지 자주 사용되는 통계를 설명합니다. 통계는 관측된 데이터의 특징을 요약한 수치를 말합니다. 대표적인 통계로는 평균, 분산, 표준편차가 있습니다. 5.8.1. 평균 평균(
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(3/4) (0) | 2021.06.19 |
|---|---|
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(2/4) (0) | 2021.06.03 |
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(1/4) (0) | 2021.05.30 |
| [딥러닝 입문 5] 확률·통계의 기초(5/5) (0) | 2021.05.15 |
| [딥러닝 입문 5] 확률·통계의 기초(3/5) (0) | 2021.02.22 |
| [딥러닝 입문 5] 확률·통계의 기초(2/5) (0) | 2021.02.12 |
| [딥러닝 입문 5] 확률·통계의 기초(1/5) (0) | 2021.01.18 |
| [딥러닝 입문 - 4] 선형 대수의 기초(9/9) (0) | 2020.07.28 |



