
이전 글에서는 설명 가능한 AI( XAI )란 무엇인가를 예를 들어서 설명하였습니다.
XAI 에는 다음과 같은 네 가지 프레임워크가 있습니다.
・출력에 대한 설명의 생성
・해석 가능 모델의 추출
・블랙박스 내용의 검사
・투명성이 있는 학습기의 설계
이번에는 표 데이터를 예로 들어,「출력에 대한 설명의 생성」의 틀로 분류되는 XAI에 대하여 알아보겠습니다. 나머지 3 개에 대해서는 다음번에 소개하겠습니다.
테이블 데이터란, 이전 글에서도 소개한 여신 심사와 같이, 어느 샘플(여신 심사의 경우는, 심사되는 측의 채무자)의「연령」,「연수」등이 표 형식으로 정리되어 있는 데이터입니다. 이번에는,「출력에 대한 설명의 생성」을 실시하는 대표적인 수법인 SHAP를 소개합니다. SHAP는 특징량과 예측값의 관계를 아는 기법이며, 특징량의 중요도를 계산할 수도 있는 편리한 기법입니다. SHAP를 설명하기 전에 특징량의 중요도를 계산하는 대표적인 방법인 Permutation Importance에 대해서도 설명합니다.
Permutation Importance
우선, 각 특징량의 중요도를 계산하는 유명한 기법인 Permutation Importance는 매우 직관적이고 알기 쉬운 수법으로 다양한 곳에서 사용되고 있습니다.
여기에서는 여신 심사를 예로 들겠습니다. 여신 심사에 있어서 AI의 활용에서는, 연수입이나 대출액등의 특징량을 이용해 그 사람이 대출을 갚을 수 있을지 어떨지를, 예측하는 것을 목적으로 합니다. 여기서 어떤 특징량이 예측 정밀도에 어떻게 연관되어 있는지 알고 싶다고 했을 때, 특징량의 중요도를 시각화 함으로써 AI 를 안심하고 사용할 수 있고, 불필요한 특징량을 제거하여 모델의 정확도를 향상할 수 있을지도 모릅니다.
Permutation Importance는, 원 데이터를 이용해 학습시킨 모델 'Mo'와 원 데이터의 어떤 특징량을 샘플 간에 랜덤 하게 재정렬한 데이터로 학습시킨 모델 'Mr'의 예측 정밀도의 차이를 계산합니다.
아래의 그림에서는 연수입이라는 특징량을 랜덤하게 바꾼 데이터로 학습한 모델과 오리지널 모델을 비교하고 있습니다. 이때, Mr과 Mr의 예측 정밀도의 차이가 큰 경우,「연수입」이라는 특징량은 예측에 중요한 특징량인 것을 알 수 있습니다. 한편, Mo와 Mr의 예측 정밀도의 차이가 작을 때「연수입」이라는 특징량의 중요도는 낮다는 것을 알 수 있습니다.

이 조작을 특징량마다 반복하여 예측 정밀도의 차이를 계산함으로써 아래 그림과 같이 특징량의 중요도를 가시화할 수 있습니다. 여기까지 가시화하면, 모델의 예측에 기여하지 않는 특징량을 삭제하거나, 인간의 판단 기준과 비교해 모델이 이상하지 않은지 체크하는 것도 가능해집니다.

SHAP
특징량의 중요도를 알았다면 다음은 각 특징량과 예측의 관계를 알고 싶어질 것입니다.
Permutation Importance에서는 어떤 특징량이 중요한지 예측 정밀도로부터 판별하였습니다. 그러나 어떤 특징량이 변화했을 때 예측이 어떻게 변화하는지 까지는 알 수 없었습니다. 예를 들어 연수입이 올라감에 따라 예측한 대출 부실률이 올라갈지 내려갈지 까지는 알 수 없었습니다.
특징량과 예측값의 관계를 알 수 있는 기법으로 SHAP(SHapley Additive exPlanations)라는 것이 있습니다. 이것은 특징량과 예측값의 관계를 볼 수 있고, 또한 특징량의 중요도로서 해석이 가능하다는 것 등, 마이크로적인 해석으로부터 매크로적인 해석까지 일관되게 실시할 수 있다는 점에서 매우 우수한 해석 기법입니다.
SHAP는 Shapley value라는 게임 이론에서 사용되는 지표를 AI 분야에 적용한 수법입니다(여담입니다만, 최근 AI를 활용해 물리학을 해석하거나, 물리학의 수법을 이용해 심층 학습 모델을 해석하는 등, 분야를 넘어선 움직임이 활발해지고 있습니다. 이러한 동향도 체크해 보시면 재미있을지도 모르겠네요). 우선은 Shapley value를 설명하고 나서, SHAP에 대해 설명하겠습니다. 다음과 같은 아르바이트 게임을 생각해 보겠습니다.
・우선, 혼자 일할 경우, A 혼자서 하면 6만 원, B 혼자서 하면 4 만원, C 혼자서 하면 2 만원을 받을 수 있다.
・그 다음으로, 2명으로 일했을 경우는,
A와 B 둘이서 했을 때는 합계 20 만원,
A와 C 둘이서 했을 때는 합계 15 만원,
B와 C 둘이서 했을 때는 합계 10 만원을 받을 수 있다.
・마지막으로, A와 B와 C 세 사람이 일하는 경우 총 24 만원을 받을 수 있다.
이것을 표로 정리하면 다음과 같습니다.

지금, A + B + C의 3 명이 일해 얻은 보수 24 만원을 어떻게 분배하는 것이 가장 공평한 것인지를 생각해 보겠습니다. 직관적으로는, 보다 공헌도가 높은 사람에게 많은 보상을 주는 것이 공평한 분배의 한 방법이 될 것 같습니다. 이 기여도를 계산하기 위해서 한계 공헌도라는 지표를 도입합니다.
이것은 협력자(플레이어)가 1 명 증가한 경우에 받을 수 있는 보상이 얼마나 커지는지를 나타내는 값입니다.
이번 경우, A 가 늘어난 경우의 한계 공헌도는
・0 명 ⇒ A의 경우 6
・B ⇒ A + B가 되어 20 - 4 = 16
・C ⇒ A + C가 되어 15 - 2 = 13
・B + C ⇒ A + B + C가 되어 24 - 10 = 14가 됩니다.
즉, A가 협력하는 타이밍에 따라 한계 공헌도는 변화한다는 것입니다. 이 효과를 상쇄하기 위해 평균적인 한계 공헌도를 생각하기로 합니다.
이것을 표에 정리하면 다음과 같습니다.

이 표에서 각 사람의 평균 한계 공헌도를 계산하면,
・A의 평균적인 한계 공헌도는 (6 + 6 + 16 + 14 + 13 + 14) / 6 = 11.5 만원
・B의 평균적인 한계 공헌도는 (14 + 9 + 4 + 4 + 9 + 8) / 6 = 8 만원
・C의 평균적인 한계 공헌도는 (4 + 9 + 4 + 6 + 2 + 2) / 6 = 4.5 만원이 됩니다.
11.5 + 8 + 4.5 = 24 만원이므로 A에게는 한계공헌도 계산으로 얻은 11.5 만원을 배분하는 것이 합리적이라고 할 수 있습니다.
이 평균적인 한계 공헌도를 Shapley value라고 합니다.
이 Shapley value를 AI 모델 해석에 사용해 봅시다. 구체적으로 다음과 같은 상황을 생각해 봅시다.
・특징량으로서, X = (X1, X2, X3)의 3 개가 존재한다.
・모델을 f 라 하면, 평균 적인 예측치는 E [f(X)] 라 한다( E는 평균을 구하는 조작을 의미 ).
・하나의 샘플의 특징량을 x = (x1, x2, x3)라 한다( 소문자 ).
이때, 어느 샘플의 특징량을 이용했을 때의 모델의 예측은 아래와 같이 나타낼 수 있습니다.

SHAP는 한 샘플에서의 예측값을 모델의 평균 예측값과 각 특징량의 기여도 Φi 의 합으로 표현하는 것을 목표로 합니다.
여기서 Shapley value를 구한 방식을 응용합니다.
각 특징량은 Shapley value에서의 협력자(플레이어)에 해당합니다. 즉, 한 샘플의 특징량 xi 를 늘리면 예측값이 얼마나 늘어나는지(감소하는지) 계산하여 각 특징량의 기여도를 계산합니다. 여기에서도 Shapley value의 계산과 마찬가지로 특징량을 늘리는 방법은 여럿이므로, 이들을 평균하여 기여도를 계산합니다.
아래 그림은 위에서 설명한 상황에서의 기여도를 나타냅니다.

이 경우 특징량 x1 을 늘릴 때 예측값은 Φ1 만큼 증가합니다. 한편, 특징량 x3 을 늘리면 예측값은 Φ3 만큼 작아집니다. 이를 통해 특정 샘플의 예측이 왜 그 값이 되는지, 특징량마다 분해해 볼 수 있습니다.
이제 암 위험 데이터를 사용하여 SHAP를 사용해 봅시다. 이 데이터에 대해 SHAP를 적용한 결과는 다음과 같습니다.

base value는 예측값의 평균이고 output value는 특정 샘플에 대한 예측값을 나타냅니다.
적색은 예측의 플러스 요인이고 청색은 마이너스 요인임을 나타냅니다.
플러스 요인과 마이너스 요인을 종합한 결과, 이 샘플에 대한 예측치는 평균보다 0.7 정도 커졌습니다.
예측치가 커진 이유로는 Age(연령)나 Smokes..years(흡연 연수)라는 특징량이 예측에 크게 기여하고 있기 때문입니다.
위의 예에서는 특정 샘플에 대한 특징량이 예측에 기여하는 방법을 보았지만, 특징량의 기여도의 평균을 취함으로써 매크로 관점에서 그 특징량이 중요한지 여부를 알 수 있었습니다. 또한, 특징량의 기여도( SHAP value )와 그 특징량의 크기를 나타낸 도표를 보는 것으로, 어느 특징량이 어떤 값일 때에, 기여도가 큰지 파악하는 것이 가능하다는 것도 알았습니다.
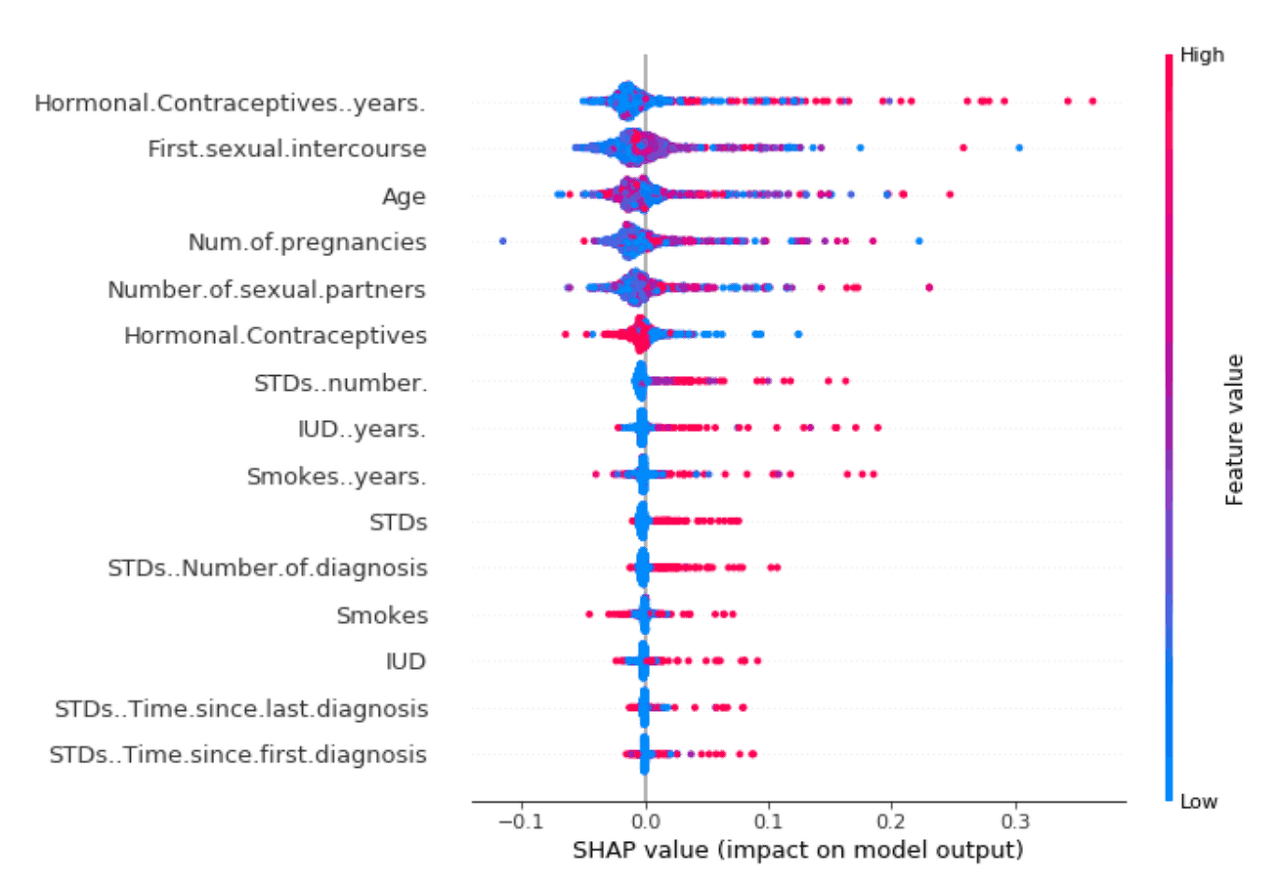
이 예제에서는 Age의 값이 클 때, 예측에 대한 기여도가 가장 큰 경향이 있다는 것을 알 수 있습니다.
요약
이번에는 XAI의 구체적인 방법으로 Permutation Importance와 SHAP라는 두 가지 유명한 방법을 알아보았습니다.
Permutation Importance는 어떤 특징량을 무작위로 바꾸어 그 특징량의 중요도를 계산하는 기법입니다.
또한, SHAP는 각 특징량의 공헌도를 Shapley value를 이용해 계산하는 것으로, 모델의 예측치와 특징량의 관계를 알 수 있고, 중요도까지 계산할 수 있는 뛰어난 알고리즘입니다. 또한, 이러한 알고리즘은 모델의 구축 방법에 관계없이 적용할 수 있으므로, 범용성이 높은 기법이라고 할 수 있습니다.
다음에는「출력에 대한 설명의 생성」으로 분류되는 XAI인 LIME에 대해 설명합니다. LIME 은 테이블 데이터뿐만 아니라 이미지 분류 모델을 해석하는 데 자주 사용되는 유명한 기술입니다.
[알기쉬운 AI - 34] 설명 가능한 AI(XAI : Explainable AI) 1 - AI의 예측에 근거는 필요한가?
설명 가능한 AI( Explainable AI, 이후 XAI )라는 단어를 들어 보신 적 있습니까? XAI는 AI 예측의 근거를 예측과 함께 출력하는 AI입니다. 특히 최근 주목을 받고 있는 심층 학습이 대두된 후 XAI의 중요성
doooob.tistory.com
[알기쉬운 AI - 36] 설명 가능한 AI(XAI : Explainable AI) 3 - 해석 가능한 모델의 추출
이전 글에서는「출력에 대한 설명의 생성」기법으로서, SHAP라고 불리는 기법을 소개했습니다. 이것은 경제학에서 사용되는 Shapley value 를 이용하여 각 특징량의 공헌도를 계산하고, 그것을 바탕
doooob.tistory.com
[알기쉬운 AI - 37] 설명 가능한 AI(XAI : Explainable AI) 4 - 블랙 박스인가 투명성인가
지금까지의 내용에서는「출력에 대한 설명의 생성」기법으로서, SHAP라고 불리는 기법을,「해석 가능한 모델의 추출」기법으로서 심층 학습 모델을 의사결정 트리로 옮겨놓거나, 모델의 예측
doooob.tistory.com
'AI · 인공지능 > 알기쉬운 AI' 카테고리의 다른 글
| [알기쉬운 AI - 39] AI 보안 2 - AI에 대한 공격 매커니즘 (3) | 2023.06.13 |
|---|---|
| [알기쉬운 AI - 38] AI 보안 1 - AI에 보안이 필요한가? (1) | 2023.03.17 |
| [알기쉬운 AI - 37] 설명 가능한 AI(XAI : Explainable AI) 4 - 블랙 박스인가 투명성인가 (0) | 2023.03.07 |
| [알기쉬운 AI - 36] 설명 가능한 AI(XAI : Explainable AI) 3 - 해석 가능한 모델의 추출 (0) | 2023.02.02 |
| [알기쉬운 AI - 34] 설명 가능한 AI(XAI : Explainable AI) 1 - AI의 예측에 근거는 필요한가? (0) | 2022.11.06 |
| [알기쉬운 AI - 33] CNN이란 어떤 것인가? (0) | 2022.10.10 |
| [알기쉬운 AI - 32] 신경망은 만능인가...? (1) | 2021.10.24 |
| [알기쉬운 AI - 31] GAN (Generative Adversarial Networks) (3) | 2020.06.07 |



