미분의 기초
3.1 미분과 함수 최소화의 관계
앞장에서 미분이 목적 함수의 최소화에 도움이 된다고 소개했습니다. 이번 장에서는 먼저 구체적인 예를 통하여 그것을 직관적으로 이해해 봅시다. 예를 들어, 아래 그림과 같이 아래로 오목한 형태를 한 함수가 어디서 최소값을 취할지 찾는 문제를 생각해 봅시다.
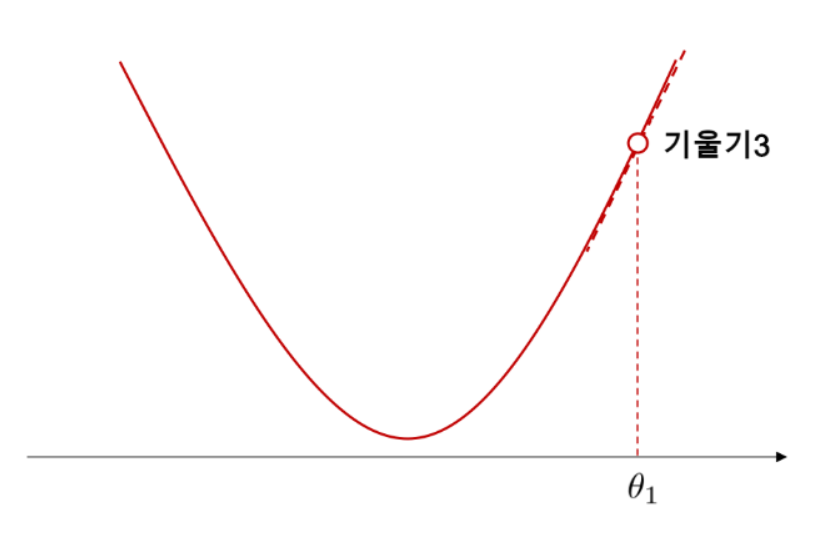
적당한 점 θ1에서 이 함수의 그래프에 접하는 직선(접선)을 살펴봅시다(※주석 1). 만일 이 접선의 기울기가 +3, 즉, 양수였다고 합시다. 이때, 접선은 오른쪽으로 갈수록 기울기가 높아지고 반대로 왼쪽으로 갈수록 낮아집니다. θ1의 주변에서는 함수의 그래프와 접선이 아주 가까워서, 점과 선의 구분이 안 될 정도입니다. 함수 역시 접선처럼 θ1의 오른쪽은 증가하고 왼쪽은 감소한다는 것을 알 수 있습니다.
(※주석 1)
이 함수의 그래프는 그래프상에 어떠한 점을 찍어도, 그 접선이 단 1개만 존재하는 상황을 고려하고 있습니다. 예를 들어, 함수의 그래프가 골짜기 부분에서 '뾰족한' 형태를 하고 있다면 골짜기의 바닥에서 여러 접선이 같은 기울기로 그려져 버립니다. 여기서는 그런 경우는 없고, 함수의 그래프가 위와 같이 '부드러운'곡선으로 되어있는 경우만 생각해 주십시오.
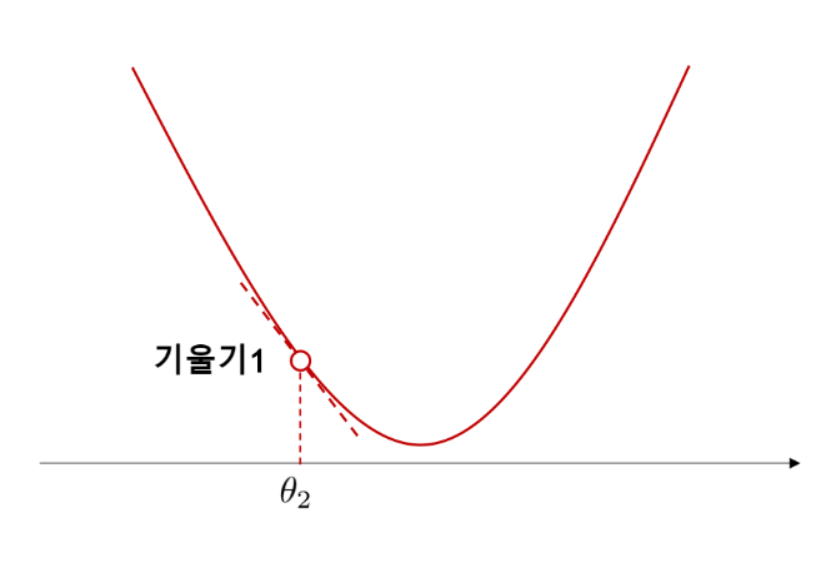
다음은 그래프상의 다른 점, θ2에서의 접선을 살펴봅시다. 이번에는 접선의 기울기가 −1이라고 합시다. 기울기가 음수이기 때문에 접선은 오른쪽으로 감소하는 직선을 그립니다. 그래프는 접선과 매우 가깝기 때문에, 그래프도 역시 θ2의 주변에서는 마찬가지로 오른쪽으로 감소한다고 볼 수 있습니다.
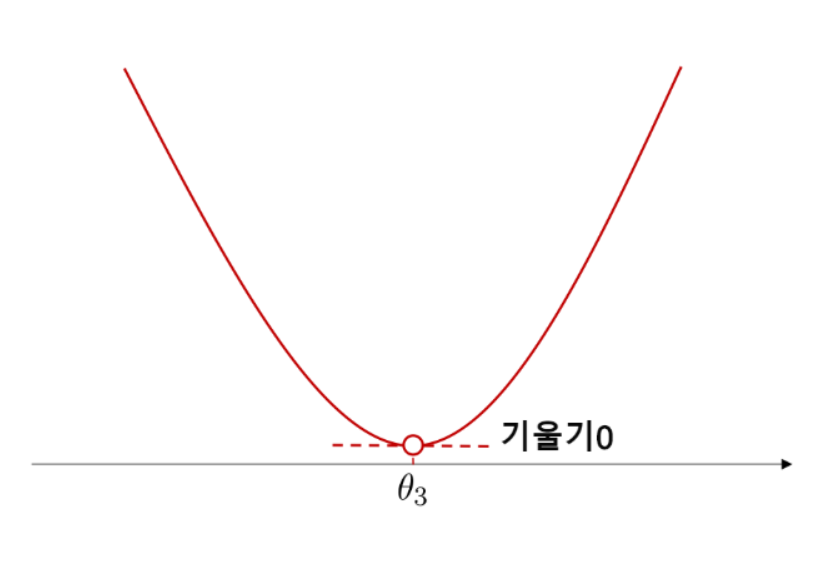
마지막으로 그래프의 골짜기 끝에 있는 점 θ3을 살펴봅시다. 그림 그대로 함수는 이 점에서 최소값을 취합니다. 한편, 점θ3에서의 접선은 수평으로, 기울기가 0입니다.
지금까지의 관찰을 정리하면, 접선의 기울기와 함수의 동작에는 다음과 같은 관계가 있음을 알 수 있습니다.
-
어느 점에 접하는 접선의 기울기가 양수라면 그 점 근처에서 그래프는 우상향(=왼쪽으로 이동하면 기울기가 감소)
-
어느 점에 접하는 접선의 기울기가 음수라면 그 점 근처에서 그래프는 우하향(=오른쪽으로 이동하면 기울기가 감소)
-
함수가 최소값을 취하는 점에 접하는 접선의 기울기는 0이다.
즉, 함수의 최소값을 취하는 점을 구하는 문제는 접선의 기울기가 0이 되는 점이 정답 후보(※주석 2)가 된다는 것을 알 수 있습니다. 이 장에서 설명하는 바와 같이, 미분을 이용하면 접선의 기울기를 계산할 수 있습니다. 이 점에서 미분이 함수의 최소화 문제에 유용한 도구임을 알 수 있습니다.
(※주석 2)
지금은 함수 그래프의 「골짜기」를 보고 있지만, 「산」에서도 마찬가지로 접선의 기울기가 0이기 때문에 한 지점에서의 접선의 기울기가 0이라고 해서 반드시 함수가 그 점에서 최소 값을 갖는 것은 아닙니다.
이상에서 미분의 정의와 미분에 관한 공식을 소개했습니다. 또한 다음에는, 입력이 여럿인 다변수 함수의 미분(편미분)에 대해서도 알아보겠습니다.
[딥러닝 입문 - 3] 미분의 기초 (2/3)
3.2. 두 점 사이를 잇는 직선의 기울기 접선의 기울기와 미분의 관계를 알아보기 위해 먼저 2점을 지나는 직선의 기울기를 구하는 문제를 봅시다. 직선의 기울기는 'y(세로)의 증가량 / x(가로)의
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 4] 선형 대수의 기초(4/9) (0) | 2020.07.18 |
|---|---|
| [딥러닝 입문 - 4] 선형 대수의 기초(3/9) (0) | 2020.07.17 |
| [딥러닝 입문 - 4] 선형 대수의 기초(2/9) (0) | 2020.07.16 |
| [딥러닝 입문 - 4] 선형 대수의 기초(1/9) (0) | 2020.07.15 |
| [딥러닝 입문 - 3] 미분의 기초 (3/3) (0) | 2020.07.12 |
| [딥러닝 입문 - 3] 미분의 기초 (2/3) (0) | 2020.07.11 |
| [딥러닝 입문 - 2] 머신 러닝에 사용되는 수학 (5) | 2020.07.07 |
| [딥러닝 입문 - 1] 딥러닝 시작하기 (0) | 2020.07.04 |



