3.2. 두 점 사이를 잇는 직선의 기울기
접선의 기울기와 미분의 관계를 알아보기 위해 먼저 2점을 지나는 직선의 기울기를 구하는 문제를 봅시다.

직선의 기울기는 'y(세로)의 증가량 / x(가로)의 증가량'으로 계산할 수 있기 때문에, 위의 직선의 기울기 a는
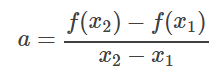
로 구할 수 있습니다.
3.3 접선의 기울기
위 그림에서 점 x1의 접선의 기울기를 구하기 위해, 다른 점 x2를 x1에 가깝게 가져갑니다. 그러나 x1과 x2가 완전히 겹치면, x 방향, y방향의 증가량이 모두 0이 되어 버리기 때문에 기울기는 0/0이 되어, 계산할 수 없습니다. 그래서 2개의 점은 다른 점으로 있으면서 x2를 한없이 x1에 가깝게 접근시켰을 때, 직선의 기울기가 어떻게 되는지를 볼 필요가 있습니다. 이를 수식으로 표현하자면 극한의 개념이 필요합니다.
극한에서는 변수가 어떤 값에 한없이 가까워질 때, 그 변수에 의해 기술되는 함수가 어떤 값에 가까워지는지를 고려합니다. 함수 f에 대하여, h라는 변수를 a에 한없이 가깝게 접근시켰을 때 f(h)가 가까워지는 값을 lim 라는 기호를 사용하여
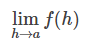
로 표현합니다. 예를 들어, h를 한없이 0에 접근시켰을 때, 3h도 한없이 0에 접근하게 됩니다. 따라서
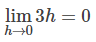
가 됩니다. 더 일반적으로 n이 자연수, c가 상수일 때,

가 성립합니다. 이것만 보면 단순히 함수

는 h에 a를 대입한 값 f(a)처럼 보일지도 모릅니다.
그러나 지금 보고 있는 직선의 기울기의 경우, 이러한 할당 작업은 아까처럼 0/0이 나오기 때문에 단순 대입으로 극한을 구할 수는 없습니다. 극한의 계산 방법은 나중에 자세히 설명하겠습니다.
그러면 아래 그림의 점 x의 접선 기울기 a를 구해봅시다.

2점을 지나는 직선의 기울기 식과 극한을 결합하여 접선의 기울기를 구할 수 있습니다.
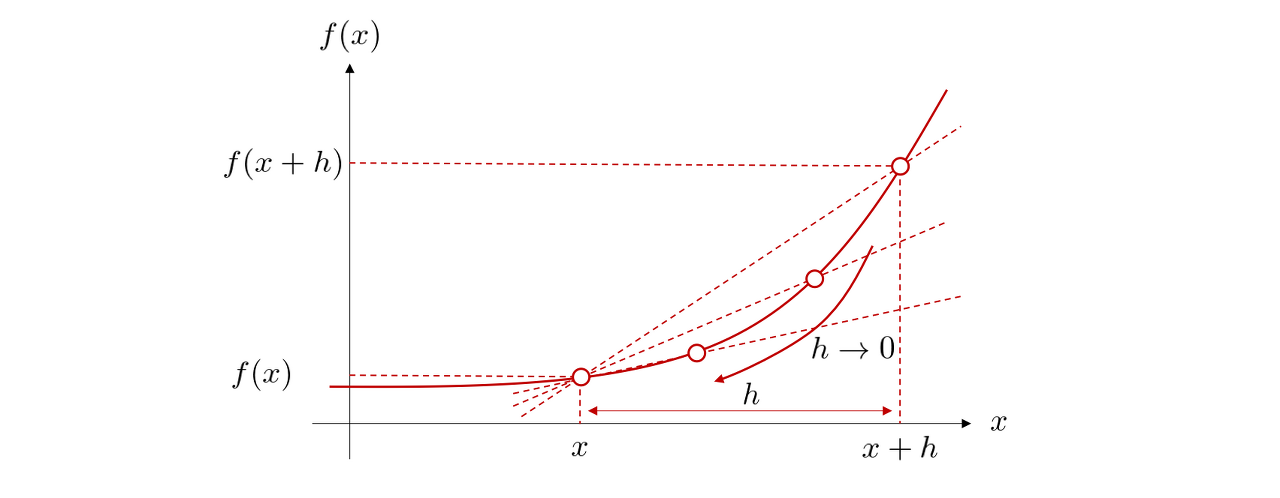
먼저, x에서 h만큼 떨어진 점 x + h가 있다고 하고, 두 점을 지나는 직선의 기울기를 구해봅시다. 그 다음 h를 0에 한없이 가깝게 하면 점 x에 접하는 접선이 될 것으로 예상이 됩니다. 이를 수식으로 보면

입니다. 잘 보면, 이 식은 x를 정하는데 어떤 하나의 값을 정하고 있습니다. 즉, 이 식은 x함수입니다(h는 h→0 의 극한을 가지고 있기 때문에, h함수는 되지 않는다는 점에 유의하십시오). 이 식을 f의 도함수(derivative)라고 부르며, f′(x)라고 씁니다. 즉,

입니다. 도함수를 구하는 것을 미분(differentiation)한다고 합니다. 기호의 사용법으로 f′(x)를

또는
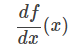
라고 써도 상관없습니다. 이 d라는 기호는 증분을 취하는 조작을 나타내며, 예를 들면 dx는 x의 변화량을 나타냅니다. 이 기법은 복잡하지만, x,y 등 변수가 여러 개인 경우, 어떤 변수로 미분하고 있는지가 명확하므로 정확한 표현이 가능합니다.
3.4 미분 공식
어느 함수의 도함수를 계산하려면 도함수의 정의대로 계산하는 것이 가장 우직한 방법입니다. 하지만 앞으로 소개하는 다양한 공식을 조합하여, 굳이 정의로 돌아가지 않아도 복잡한 함수의 도함수를 계산할 수 있습니다. 다음의 c는 상수, x는 변수를 나타냅니다. 우선, 다음의 3개의 공식을 소개합니다.

첫 번째 좌변은 상수 함수 f(x) = c를 x로 미분한 도함수를 나타냅니다. 상수 함수의 그래프를 작성하면 x축에 평행하므로 어떤 점에서 접선을 그어도 그 기울기는 0입니다(그래프와 접선은 동일한 직선이 됩니다). 이것은 도함수가 0 임을 의미합니다. 이것이 첫 번째 식의 도형적인 이해입니다. 마찬가지로 두 번째 공식은 'y=x의 그래프는 어떤 점에서 접선을 그어도 기울기가 1'인 것을 의미합니다(이 경우도 그래프와 접선은 동일한 직선입니다). 극한의 취급에 익숙해지기 위해 세 번째 공식을 증명해 봅시다. 도함수의 정의에서 좌변은

으로 계산할 수 있습니다. 여기에서 h→0, 즉, h를 한없이 0에 접근시키면, 2x+h는 2x에 한없이 가까워집니다.
따라서,(x제곱)′=2x가 구해졌습니다.
다음 공식도 자주 이용합니다.

여기에서 a는 상수, e는 자연로그의 밑이나 네이피어의 수라는 특별한 상수로, 약 2.71828...입니다. 첫 번째 공식에서 n=1,2라면, 처음 소개한 x, x제곱의 미분 공식으로 귀착된다는 점에 유의하십시오. e의 ax승은 exp(ax)처럼 표기되는 경우가 많습니다. 그 표기를 사용하면 마지막 공식은
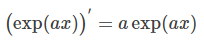
라고도 쓸 수 있습니다.
[딥러닝 입문 - 3] 미분의 기초 (3/3)
3.5 선형성 미분은 선형성이라는 성질을 가지고 있습니다. 구체적인 예를 들어 살펴봅시다. 처럼 상수를 미분 연산의 외측으로 꺼낼 수 있습니다. 또한, 처럼, 덧셈과 뺄셈은 각 항목마다 독립적
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| [딥러닝 입문 - 4] 선형 대수의 기초(4/9) (0) | 2020.07.18 |
|---|---|
| [딥러닝 입문 - 4] 선형 대수의 기초(3/9) (0) | 2020.07.17 |
| [딥러닝 입문 - 4] 선형 대수의 기초(2/9) (0) | 2020.07.16 |
| [딥러닝 입문 - 4] 선형 대수의 기초(1/9) (0) | 2020.07.15 |
| [딥러닝 입문 - 3] 미분의 기초 (3/3) (0) | 2020.07.12 |
| [딥러닝 입문 - 3] 미분의 기초 (1/3) (1) | 2020.07.10 |
| [딥러닝 입문 - 2] 머신 러닝에 사용되는 수학 (5) | 2020.07.07 |
| [딥러닝 입문 - 1] 딥러닝 시작하기 (0) | 2020.07.04 |



