6.2 다중 회귀 분석(multiple regression analysis)
6.2.1. 문제 설정 (다중 회귀 분석)
다중 회귀 분석도 단일 회귀 분석의 경우와 마찬가지로 임대료를 예측하는 문제로 설명하겠습니다. 단일 회귀 분석의 경우와 달리, 입력 변수로 '방 넓이' 뿐만 아니라 '역세권'이나 '범죄율'등의 변수를 함께 고려합니다. 방의 넓이를 x1, 역과의 거리를 x2, 범죄율을 xM 같은 형태로 나타내며, M개의 입력 변수를 취급하는 것을 생각해 봅시다.
6.2.2. Step 1 : 모델을 결정(다중 회귀 분석)
단일 회귀 분석에서는,

와 같이 직선의 방정식을 모델로 사용했습니다. 다중 회귀 분석에서도
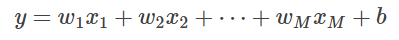
와 같이 단일 회귀 분석과 비슷한 모델을 정의합니다. 단일 회귀 분석 시엔 이차원 평면을 생각하고 그 평면상에 존재하는 데이터에 가장 알맞은 직선을 찾았지만, 이번에는 M차원 공간에 존재하는 데이터에 가장 알맞은 직선을 찾습니다.
다중 회귀 분석 모델은 시그마 기호를 사용해 표기하면

로 표기할 수 있습니다.
여기서 바이어스 b의 처리 방법을 다시 생각해 봅시다. 단일 회귀 분석에서는 중심화를 전처리로 실시하여 바이어스 b를 생략하여 간결하게 정의할 수 있었습니다.
다중 회귀 분석에서는 M개의 가중치 w1, w2, …, wM과 1개의 바이어스 b가 있어, 총 M+1개의 매개 변수가 존재합니다. 이러한 매개 변수를 공식화하는 것을 생각해 봅시다.
그래서 이번에는 x0=1, w0=b로 두면,
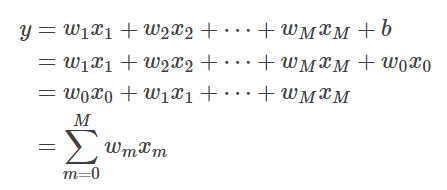
처럼 b를 총합의 내부 섹션에 포함하여 간결하게 표기할 수 있습니다.
(여기서, ∑기호의 하단이 m=1 이 아니라, m=0이라는 점에 유의하십시오. )
또한 여기에서 선형 대수학에서 배운 지식을 활용하여 수식을 정리하고 있습니다. 위 식을 벡터의 내적을 이용하여 다시 표기하면

같이 간단한 형식으로 표현할 수 있습니다. 이 모델이 가지는 파라미터는 M+1개 있으며, M+1차원 벡터 w로 표시되어 있습니다. 다중 회귀 분석에서는 이 w의 모든 요소에 대해 최적의 값을 구합니다.
6.2.3. Step 2 : 목적 함수를 결정(다중 회귀 분석)
단일 회귀 분석의 예와 비교하면, 입력 변수는 증가했지만 임대료를 목표로 하고 있다는 점은 변함이 없습니다. 그래서 단일 회귀 분석과 동일한 목적 함수
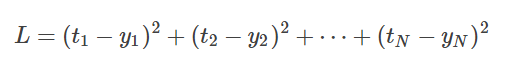
를 사용합니다. 이 목적 함수는 벡터의 내적을 이용하여 다시 표기하면,
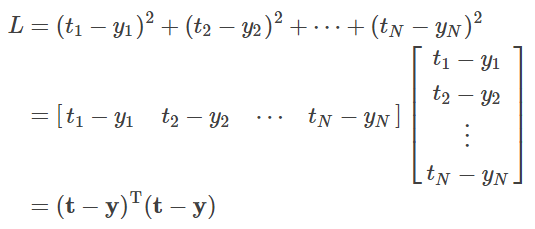
라고 표기할 수 있습니다.
여기서, 내적은 교환 법칙이 성립하므로 wTx는 xTw라고 쓸 수 있습니다. 이를 이용하여 모델의 방정식 y=wTx를 다음과 같이 변형합니다.

또한,
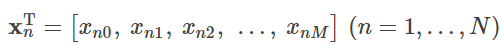
로 전개하면

로 표기할 수 있습니다. 여기에서 N×M 행렬 X는, 각 행이 각 데이터를 나타내며 각 열은 각 입력 변수를 나타냅니다. 이러한 행렬을 디자인 행렬(design matrix)이라고 합니다. 각 열은 각 입력 변수의 종류에 대응하고, 예를 들면 방의 넓이 나 역에서의 거리 등입니다.
각 행이 나타내는 데이터 포인트가 어떻게 표현되고 있는지를 설명하기 위해, 구체적인 수치로 예를 들겠습니다.
방의 넓이 : 50 제곱미터
역에서의 거리 : 600 미터
범죄율 : 2%
이렇게 세 개의 입력 변수를 고려한다면, M=3이며, 이것이 n개째인 데이터의 경우,

가 됩니다. 맨 앞에 1이 있는 것은 Step 1로 x0=1이라 정했기 때문입니다.
[딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(4/4)
6.2.4. Step 3 : 매개 변수를 최적화하기 (회귀 분석) 그럼, 목적 함수 L을 최소화하는 모델의 파라미터 벡터 w를 구해 봅시다. 단일 회귀 분석과 마찬가지로 목적 함수를 매개 변수로 미분하여 0으
doooob.tistory.com
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| 딥 러닝을 이용한 자연어 처리 입문 (0) | 2021.08.09 |
|---|---|
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(4/4) (0) | 2021.07.31 |
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(2/4) (0) | 2021.06.03 |
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(1/4) (0) | 2021.05.30 |
| [딥러닝 입문 5] 확률·통계의 기초(5/5) (0) | 2021.05.15 |
| [딥러닝 입문 5] 확률·통계의 기초(4/5) (0) | 2021.03.09 |
| [딥러닝 입문 5] 확률·통계의 기초(3/5) (0) | 2021.02.22 |
| [딥러닝 입문 5] 확률·통계의 기초(2/5) (0) | 2021.02.12 |



