6.2.4. Step 3 : 매개 변수를 최적화하기 (회귀 분석)
그럼, 목적 함수 L을 최소화하는 모델의 파라미터 벡터 w를 구해 봅시다. 단일 회귀 분석과 마찬가지로 목적 함수를 매개 변수로 미분하여 0으로 두고, w에 대하여 구합니다.
우선 목적 함수에 등장하고 있는 예측치 y를, 매개 변수 w를 이용한 표기로 바꿔줍니다.

여기에서 전치의 공식

를 사용했습니다. 또한 분배 법칙을 사용하여 식을 전개하면

가 됩니다. 이 목적 함수에 매개 변수 w에 대한 편미분을 계산합니다.
그전에, 이 식을 좀 더 정리합니다. 우선,

처럼 스칼라는 전치해도 변하지 않습니다. 또한,

이며,

가 되기 때문에,

사이의 내적
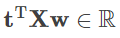
는 스칼라가 됩니다. 따라서,

가 성립합니다. 또한 전치의 공식
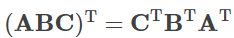
에 의해

도 성립됩니다. 이로부터
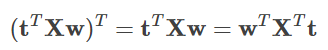
가 얻어집니다. 목적 함수
L은 이 식을 이용하여

로 변형할 수 있습니다. 여기서 w에 대한 편미분을 쉽게 하려면, w 이외의 정수 부분을 하나로 묶어줍니다.

그러면, w에 대한 이차 형식으로 표현이 가능합니다. 여기에서
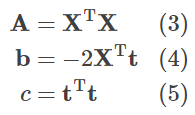
라는 점에 유의하십시오.
그럼, 목적 함수를 최소화하는 매개 변수 w를 구하는 방법을 생각해 보겠습니다. 목적 함수는 매개 변수 w에 대한 이차 함수로 되어 있습니다. 우선 w 이외의 벡터나 행렬에 구체적인 수치를 적용시켜 생각해 봅시다. 예를 들어,

로 두면, 목적 함수의 값은
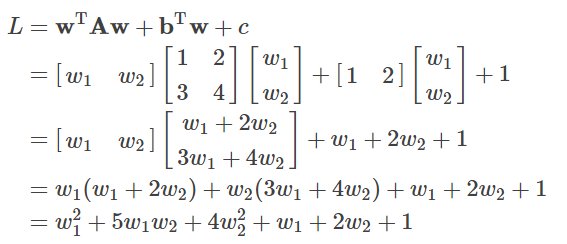
입니다. 이를 w1, w2에 대하여 정리하면

가 되고, w1, w2 각각의 이차 함수가 되어 있다는 것을 알 수 있습니다.
목적 함수 L을 w1의 이차 함수, w2의 이차 함수로 보았을 때, L은 아래 그림과 같이 됩니다.

또한 각 차원이 w1, w2, L을 나타내는 3차원 공간에 있어서는, L은 아래와 같습니다.

여기에서는 두 개의 매개 변수 w1과 w2에 대하여 그려 보이고 있지만, 목적 함수가 임의의 M개 변수 w0, w1, w2,…, wM에 의해 특징지어지는 경우에도, 목적 함수가 각각의 매개 변수에 대한 이차 형식으로 되어있는 한, 같은 모양이라고 할 수 있습니다. 즉 M+1개의 연립 방정식,

을 풀면 된다는 것입니다. 이것은 벡터에 의한 미분을 이용하여 표기하면 다음과 같이 됩니다.

위 식을 w에 대하여 풀기 위해 다음과 같이 식을 변형합니다. 식 변형 도중에 이해할 수 없는 부분이 있을 경우는, 여기를 다시 읽어보십시오. 먼저 좌변에 대해서 정리합니다.
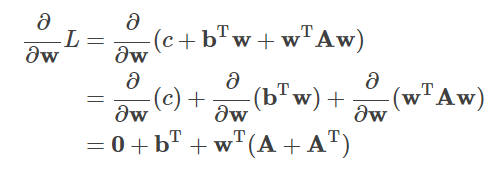
이것을 0으로 두고, A, b를 전개하면

와 같이 식 변형이 가능합니다. 여기서 양변을 전치하고

의 전치를 고쳐둡시다.

여기에서 xTx에 역행렬이 존재한다고 가정하고 양변에 왼쪽부터

를 곱하면

로 정리됩니다. 특히, 이 마지막 표현식을 정규 방정식(normal equation)이라고 합니다. 위 식은 주어진 데이터를 정렬한 디자인 행렬 X와, 각 데이터의 목표치를 늘어놓은 벡터 t로부터 최적의 매개 변수 w를 계산하고 있습니다. I(아이)는 단위행렬을 나타냅니다.
w를 도출할 때 주의해야 할 것으로, 다음의 잘못된 식 변형을 예로 들 수 있습니다.

위의 식 변형은 일반적으로 성립하지 않습니다. 이 식 변형이 가능한지 여부는
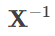
가 존재하는지 여부와 관련 있습니다.
샘플 사이즈 N과 독립 변수의 수 M+1이 같지 않으면

는 정방 행렬(행과 열의 수가 같은 행렬)이 아니기 때문에, 역행렬
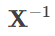
을 갖지 않습니다.
따라서 위 식의 두 번째 행의 변형은 불가합니다.(역행렬을 구하기 위한 더 엄격한 조건은 여기에서는 생략합니다.)
한편, xTx는 (M+1) × (M+1) 행렬이며, 그 형태는 샘플 사이즈 N에 의존하지 않고 항상 정방 행렬이 되기 때문에 이를 이용하여 식을 변형합니다. 새로운 입력 변수의 값
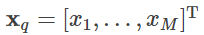
에 대하여 대응하는 목표치 yq를 예측하기 위해서는, 훈련에 의해 결정된 매개 변수 w를 준비하여

와 같이 계산합니다.
'AI · 인공지능 > 딥러닝 Tutorial' 카테고리의 다른 글
| 딥 러닝을 이용한 자연어 처리 입문 (0) | 2021.08.09 |
|---|---|
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(3/4) (0) | 2021.06.19 |
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(2/4) (0) | 2021.06.03 |
| [딥러닝 입문 - 6] 단일 회귀 분석과 다중 회귀 분석(1/4) (0) | 2021.05.30 |
| [딥러닝 입문 5] 확률·통계의 기초(5/5) (0) | 2021.05.15 |
| [딥러닝 입문 5] 확률·통계의 기초(4/5) (0) | 2021.03.09 |
| [딥러닝 입문 5] 확률·통계의 기초(3/5) (0) | 2021.02.22 |
| [딥러닝 입문 5] 확률·통계의 기초(2/5) (0) | 2021.02.12 |



